Dynamic categories, dynamic operads: From deep learning to prediction markets

Natural organized systems adapt to internal and external pressures and this seems to happens all the way down. Wanting to think clearly about this idea motivates our paper, and so the idea is elaborated extensively in the introduction, which should be broadly accessible to a philosophically-interested audience. In the remaining sections, we turn to more compressed category theory. We define the monoidal double category $\mathbf{Org}$ of dynamic organizations, we provide definitions of $\mathbf{Org}$-enriched, or "dynamic", categorical structures -- e.g. dynamic categories, operads, and monoidal categories -- and we show how they instantiate the motivating philosophical ideas. We give two examples of dynamic categorical structures: prediction markets as a dynamic operad and deep learning as a dynamic monoidal category.

Deep neural networks as nested dynamical systems

There is an analogy that is often made between deep neural networks and actual brains, suggested by the nomenclature itself: the "neurons" in deep neural networks should correspond to neurons (or nerve cells, to avoid confusion) in the brain. We claim, however, that this analogy doesn't even type check: it is structurally flawed. In agreement with the slightly glib summary of Hebbian learning as "cells that fire together wire together", this article makes the case that the analogy should be different. Since the "neurons" in deep neural networks are managing the changing weights, they are more akin to the synapses in the brain; instead, it is the wires in deep neural networks that are more like nerve cells, in that they are what cause the information to flow. An intuition that nerve cells seem like more than mere wires is exactly right, and is justified by a precise category-theoretic analogy which we will explore in this article. Throughout, we will continue to highlight the error in equating artificial neurons with nerve cells by leaving "neuron" in quotes or by calling them artificial neurons. We will first explain how to view deep neural networks as nested dynamical systems with a very restricted sort of interaction pattern, and then explain a more general sort of interaction for dynamical systems that is useful throughout engineering, but which fails to adapt to changing circumstances. As mentioned, an analogy is then forced upon us by the mathematical formalism in which they are both embedded. We call the resulting encompassing generalization deeply interacting learning systems: they have complex interaction as in control theory, but adaptation to circumstances as in deep neural networks.

Learners' languages

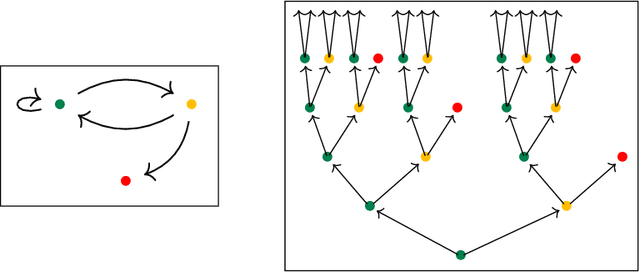
In "Backprop as functor", the authors show that the fundamental elements of deep learning -- gradient descent and backpropagation -- can be conceptualized as a strong monoidal functor $\mathbf{Para}(\mathbf{Euc})\to\mathbf{Learn}$ from the category of parameterized Euclidean spaces to that of learners, a category developed explicitly to capture parameter update and backpropagation. It was soon realized that there is an isomorphism $\mathbf{Learn}\cong\mathbf{Para}(\mathbf{SLens})$, where $\mathbf{SLens}$ is the symmetric monoidal category of simple lenses as used in functional programming. In this note, we observe that $\mathbf{SLens}$ is a full subcategory of $\mathbf{Poly}$, the category of polynomial functors in one variable, via the functor $A\mapsto Ay^A$. Using the fact that $(\mathbf{Poly},\otimes)$ is monoidal closed, we show that a map $A\to B$ in $\mathbf{Para}(\mathbf{SLens})$ has a natural interpretation in terms of dynamical systems (more precisely, generalized Moore machines) whose interface is the internal-hom type $[Ay^A,By^B]$. Finally, we review the fact that the category $p\text{-}\mathbf{Coalg}$ of dynamical systems on any $p\in\mathbf{Poly}$ forms a topos, and consider the logical propositions that can be stated in its internal language. We give gradient descent as an example, and we conclude by discussing some directions for future work.

A Compositional Sheaf-Theoretic Framework for Event-Based Systems

A compositional sheaf-theoretic framework for the modeling of complex event-based systems is presented. We show that event-based systems are machines, with inputs and outputs, and that they can be composed with machines of different types, all within a unified, sheaf-theoretic formalism. We take robotic systems as an exemplar of complex systems and rigorously describe actuators, sensors, and algorithms using this framework.

Monitoring and Diagnosability of Perception Systems

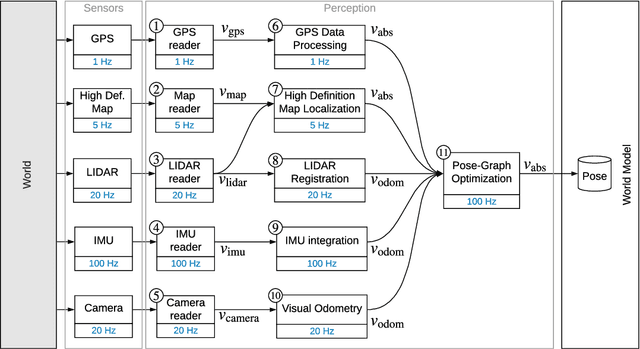
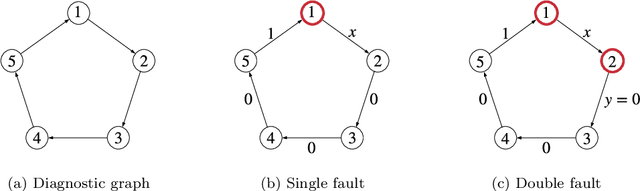
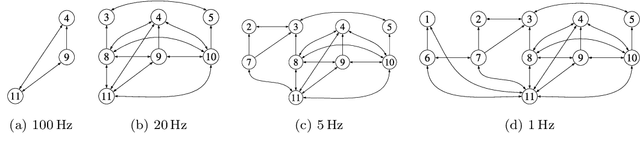
Perception is a critical component of high-integrity applications of robotics and autonomous systems, such as self-driving vehicles. In these applications, failure of perception systems may put human life at risk, and a broad adoption of these technologies requires the development of methodologies to guarantee and monitor safe operation. Despite the paramount importance of perception systems, currently there is no formal approach for system-level monitoring. In this work, we propose a mathematical model for runtime monitoring and fault detection and identification in perception systems. Towards this goal, we draw connections with the literature on diagnosability in multiprocessor systems, and generalize it to account for modules with heterogeneous outputs that interact over time. The resulting temporal diagnostic graphs (i) provide a framework to reason over the consistency of perception outputs -- across modules and over time -- thus enabling fault detection, (ii) allow us to establish formal guarantees on the maximum number of faults that can be uniquely identified in a given perception system, and (iii) enable the design of efficient algorithms for fault identification. We demonstrate our monitoring system, dubbed PerSyS, in realistic simulations using the LGSVL self-driving simulator and the Apollo Auto autonomy software stack, and show that PerSyS is able to detect failures in challenging scenarios (including scenarios that have caused self-driving car accidents in recent years), and is able to correctly identify faults while entailing a minimal computation overhead (< 5ms on a single-core CPU).

Backprop as Functor: A compositional perspective on supervised learning

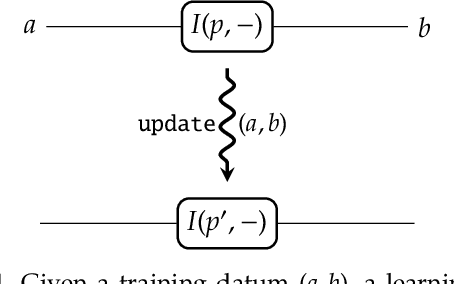
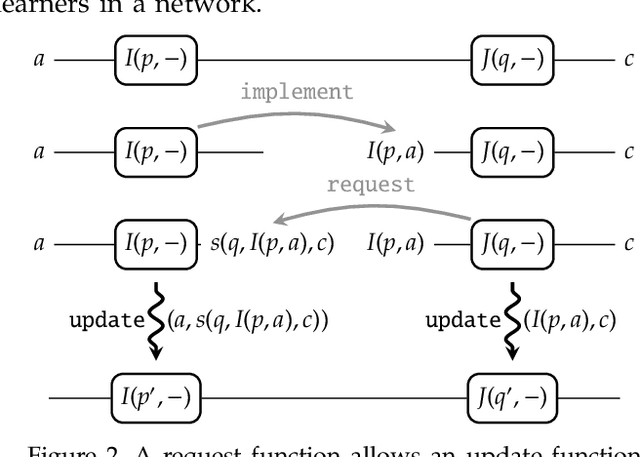
A supervised learning algorithm searches over a set of functions $A \to B$ parametrised by a space $P$ to find the best approximation to some ideal function $f\colon A \to B$. It does this by taking examples $(a,f(a)) \in A\times B$, and updating the parameter according to some rule. We define a category where these update rules may be composed, and show that gradient descent---with respect to a fixed step size and an error function satisfying a certain property---defines a monoidal functor from a category of parametrised functions to this category of update rules. This provides a structural perspective on backpropagation, as well as a broad generalisation of neural networks.

Ologs: a categorical framework for knowledge representation

In this paper we introduce the olog, or ontology log, a category-theoretic model for knowledge representation (KR). Grounded in formal mathematics, ologs can be rigorously formulated and cross-compared in ways that other KR models (such as semantic networks) cannot. An olog is similar to a relational database schema; in fact an olog can serve as a data repository if desired. Unlike database schemas, which are generally difficult to create or modify, ologs are designed to be user-friendly enough that authoring or reconfiguring an olog is a matter of course rather than a difficult chore. It is hoped that learning to author ologs is much simpler than learning a database definition language, despite their similarity. We describe ologs carefully and illustrate with many examples. As an application we show that any primitive recursive function can be described by an olog. We also show that ologs can be aligned or connected together into a larger network using functors. The various methods of information flow and institutions can then be used to integrate local and global world-views. We finish by providing several different avenues for future research.