A category theoretical argument for causal inference

The goal of this paper is to design a causal inference method accounting for complex interactions between causal factors. The proposed method relies on a category theoretical reformulation of the definitions of dependent variables, independent variables and latent variables in terms of products and arrows in the category of unlabeled partitions. Throughout the paper, we demonstrate how the proposed method accounts for possible hidden variables, such as environmental variables or noise, and how it can be interpreted statistically in terms of $p$-values. This interpretation, from category theory to statistics, is implemented through a collection of propositions highlighting the functorial properties of ANOVA. We use these properties in combination with our category theoretical framework to provide solutions to causal inference problems with both sound algebraic and statistical properties. As an application, we show how the proposed method can be used to design a combinatorial genome-wide association algorithm for the field of genetics.

Backprop as Functor: A compositional perspective on supervised learning

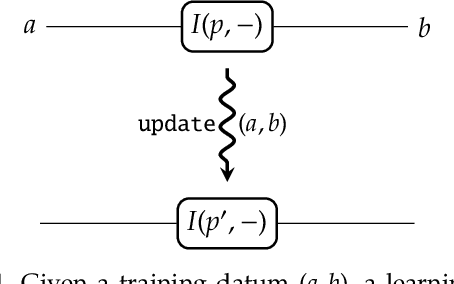
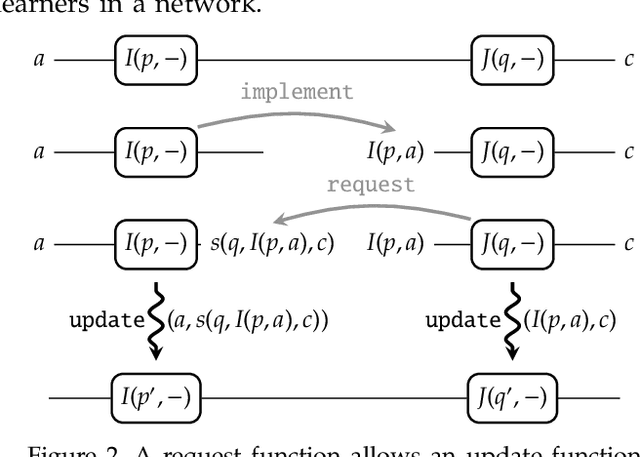
A supervised learning algorithm searches over a set of functions $A \to B$ parametrised by a space $P$ to find the best approximation to some ideal function $f\colon A \to B$. It does this by taking examples $(a,f(a)) \in A\times B$, and updating the parameter according to some rule. We define a category where these update rules may be composed, and show that gradient descent---with respect to a fixed step size and an error function satisfying a certain property---defines a monoidal functor from a category of parametrised functions to this category of update rules. This provides a structural perspective on backpropagation, as well as a broad generalisation of neural networks.