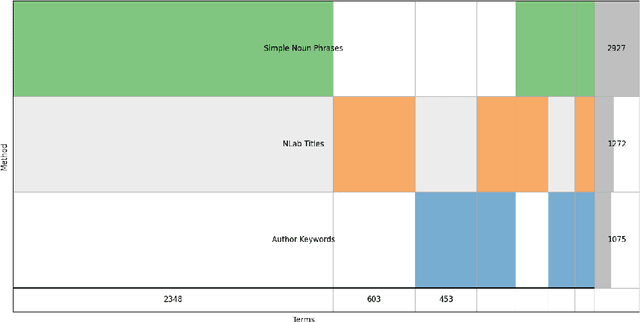
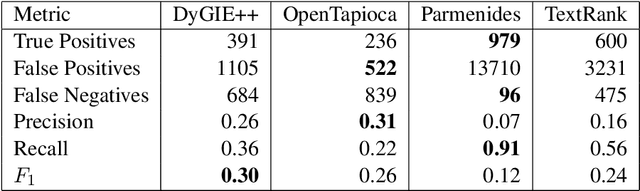
Extracting Mathematical Concepts from Text

We investigate different systems for extracting mathematical entities from English texts in the mathematical field of category theory as a first step for constructing a mathematical knowledge graph. We consider four different term extractors and compare their results. This small experiment showcases some of the issues with the construction and evaluation of terms extracted from noisy domain text. We also make available two open corpora in research mathematics, in particular in category theory: a small corpus of 755 abstracts from the journal TAC (3188 sentences), and a larger corpus from the nLab community wiki (15,000 sentences).

Lenses and Learners

Lenses are a well-established structure for modelling bidirectional transformations, such as the interactions between a database and a view of it. Lenses may be symmetric or asymmetric, and may be composed, forming the morphisms of a monoidal category. More recently, the notion of a learner has been proposed: these provide a compositional way of modelling supervised learning algorithms, and again form the morphisms of a monoidal category. In this paper, we show that the two concepts are tightly linked. We show both that there is a faithful, identity-on-objects symmetric monoidal functor embedding a category of asymmetric lenses into the category of learners, and furthermore there is such a functor embedding the category of learners into a category of symmetric lenses.

Backprop as Functor: A compositional perspective on supervised learning

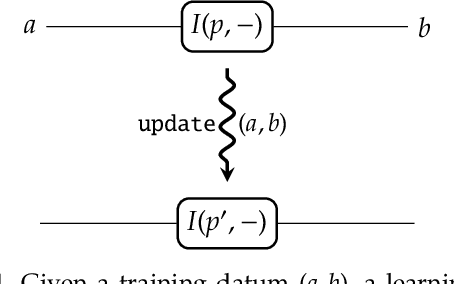
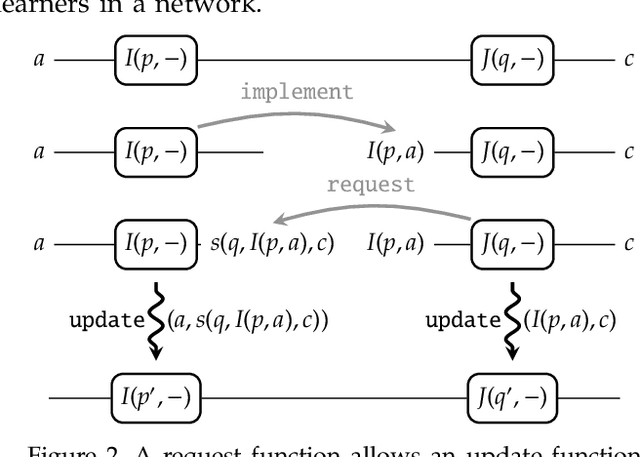
A supervised learning algorithm searches over a set of functions $A \to B$ parametrised by a space $P$ to find the best approximation to some ideal function $f\colon A \to B$. It does this by taking examples $(a,f(a)) \in A\times B$, and updating the parameter according to some rule. We define a category where these update rules may be composed, and show that gradient descent---with respect to a fixed step size and an error function satisfying a certain property---defines a monoidal functor from a category of parametrised functions to this category of update rules. This provides a structural perspective on backpropagation, as well as a broad generalisation of neural networks.