Soft Concept Analysis

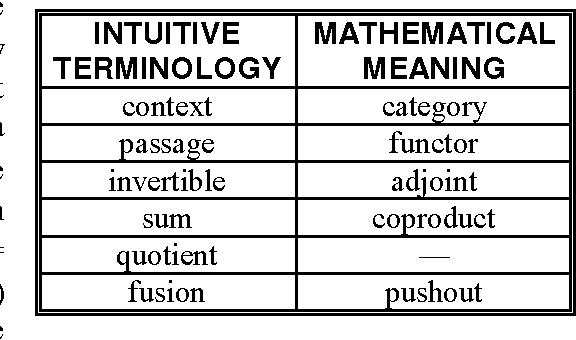
In this chapter we discuss soft concept analysis, a study which identifies an enriched notion of "conceptual scale" as developed in formal concept analysis with an enriched notion of "linguistic variable" as discussed in fuzzy logic. The identification "enriched conceptual scale" = "enriched linguistic variable" was made in a previous paper (Enriched interpretation, Robert E. Kent). In this chapter we offer further arguments for the importance of this identification by discussing the philosophy, spirit, and practical application of conceptual scaling to the discovery, conceptual analysis, interpretation, and categorization of networked information resources. We argue that a linguistic variable, which has been defined at just the right generalization of valuated categories, provides a natural definition for the process of soft conceptual scaling. This enrichment using valuated categories models the relation of indiscernability, a notion of central importance in rough set theory. At a more fundamental level for soft concept analysis, it also models the derivation of formal concepts, a process of central importance in formal concept analysis. Soft concept analysis is synonymous with enriched concept analysis. From one viewpoint, the study of soft concept analysis that is initiated here extends formal concept analysis to soft computational structures. From another viewpoint, soft concept analysis provides a natural foundation for soft computation by unifying and explaining notions from soft computation in terms of suitably generalized notions from formal concept analysis, rough set theory and fuzzy set theory.

Enriched Interpretation

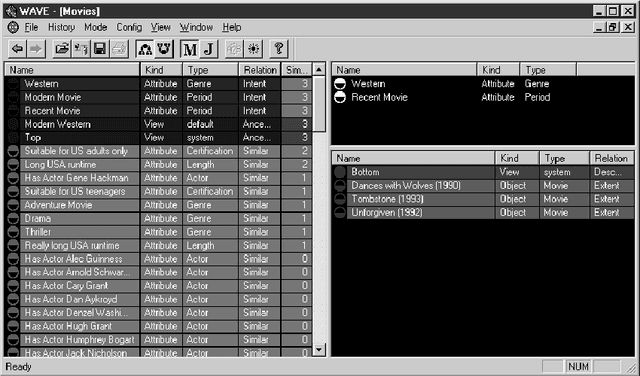
The theory introduced, presented and developed in this paper, is concerned with an enriched extension of the theory of Rough Sets pioneered by Zdzislaw Pawlak. The enrichment discussed here is in the sense of valuated categories as developed by F.W. Lawvere. This paper relates Rough Sets to an abstraction of the theory of Fuzzy Sets pioneered by Lotfi Zadeh, and provides a natural foundation for "soft computation". To paraphrase Lotfi Zadeh, the impetus for the transition from a hard theory to a soft theory derives from the fact that both the generality of a theory and its applicability to real-world problems are substantially enhanced by replacing various hard concepts with their soft counterparts. Here we discuss the corresponding enriched notions for indiscernibility, subsets, upper/lower approximations, and rough sets. Throughout, we indicate linkages with the theory of Formal Concept Analysis pioneered by Rudolf Wille. We pay particular attention to the all-important notion of a "linguistic variable" - developing its enriched extension, comparing it with the notion of conceptual scale from Formal Concept Analysis, and discussing the pragmatic issues of its creation and use in the interpretation of data. These pragmatic issues are exemplified by the discovery, conceptual analysis, interpretation, and categorization of networked information resources in WAVE, the Web Analysis and Visualization Environment currently being developed for the management and interpretation of the universe of resource information distributed over the World-Wide Web.

The Information Flow Foundation for Conceptual Knowledge Organization

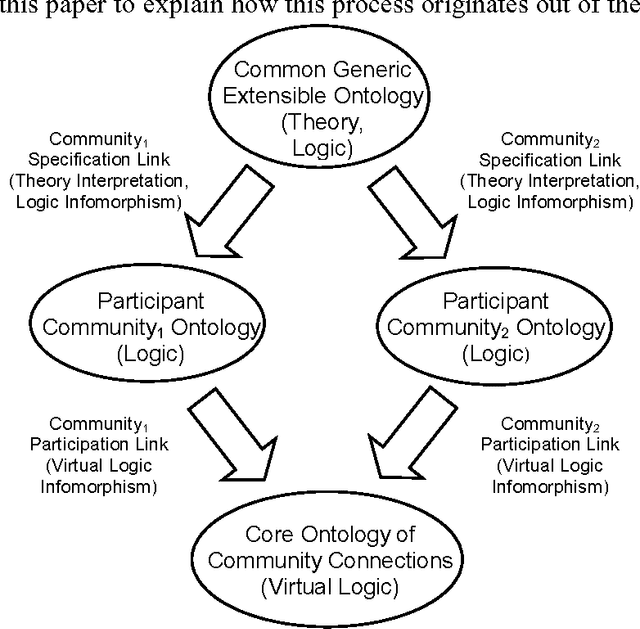
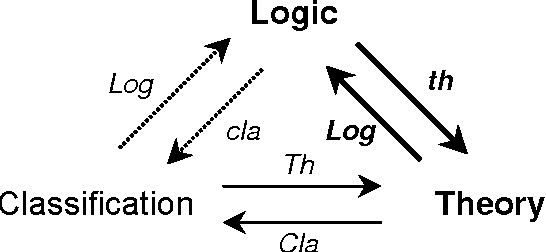
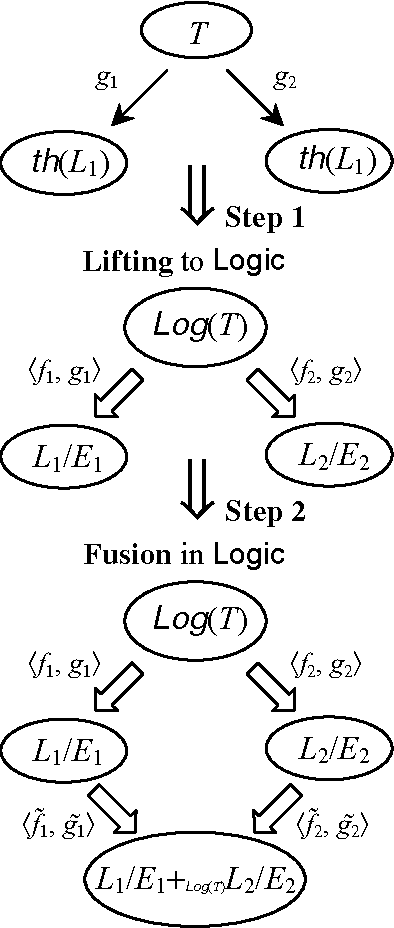
The sharing of ontologies between diverse communities of discourse allows them to compare their own information structures with that of other communities that share a common terminology and semantics - ontology sharing facilitates interoperability between online knowledge organizations. This paper demonstrates how ontology sharing is formalizable within the conceptual knowledge model of Information Flow (IF). Information Flow indirectly represents sharing through a specifiable, ontology extension hierarchy augmented with synonymic type equivalencing - two ontologies share terminology and meaning through a common generic ontology that each extends. Using the paradigm of participant community ontologies formalized as IF logics, a common shared extensible ontology formalized as an IF theory, participant community specification links from the common ontology to the participating community ontology formalizable as IF theory interpretations, this paper argues that ontology sharing is concentrated in a virtual ontology of community connections, and demonstrates how this virtual ontology is computable as the fusion of the participant ontologies - the quotient of the sum of the participant ontologies modulo the ontological sharing structure.

Semantic Integration in the Information Flow Framework

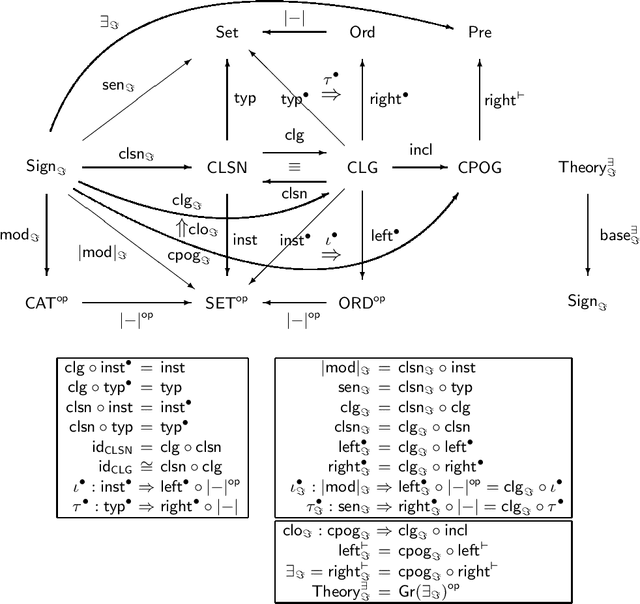
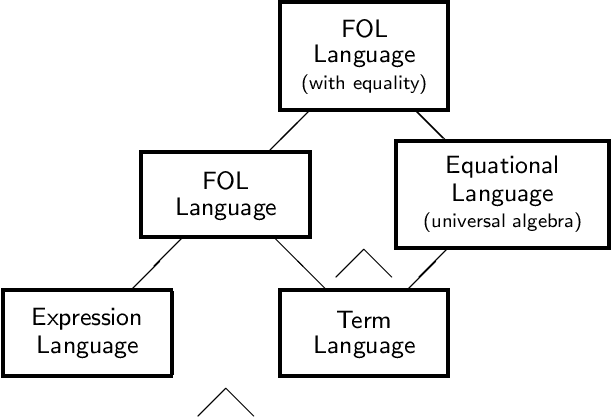
The Information Flow Framework (IFF) is a descriptive category metatheory currently under development, which is being offered as the structural aspect of the Standard Upper Ontology (SUO). The architecture of the IFF is composed of metalevels, namespaces and meta-ontologies. The main application of the IFF is institutional: the notion of institutions and their morphisms are being axiomatized in the upper metalevels of the IFF, and the lower metalevel of the IFF has axiomatized various institutions in which semantic integration has a natural expression as the colimit of theories.

The Institutional Approach

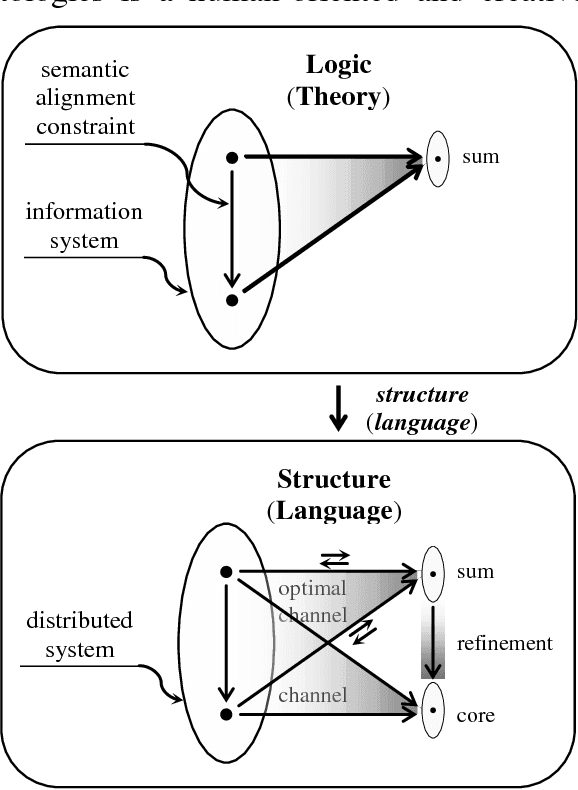
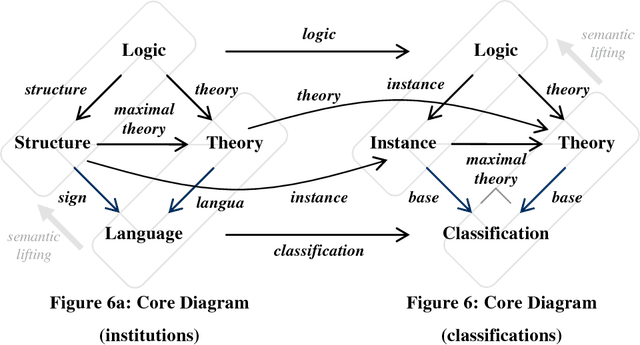
This chapter discusses the institutional approach for organizing and maintaining ontologies. The theory of institutions was named and initially developed by Joseph Goguen and Rod Burstall. This theory, a metatheory based on category theory, regards ontologies as logical theories or local logics. The theory of institutions uses the category-theoretic ideas of fibrations and indexed categories to develop logical theories. Institutions unite the lattice approach of Formal Concept Analysis of Ganter and Wille with the distributed logic of Information Flow of Barwise and Seligman. The institutional approach incorporates locally the lattice of theories idea of Sowa from the theory of knowledge representation. The Information Flow Framework, which was initiated within the IEEE Standard Upper Ontology project, uses the institutional approach in its applied aspect for the comparison, semantic integration and maintenance of ontologies. This chapter explains the central ideas of the institutional approach to ontologies in a careful and detailed manner.

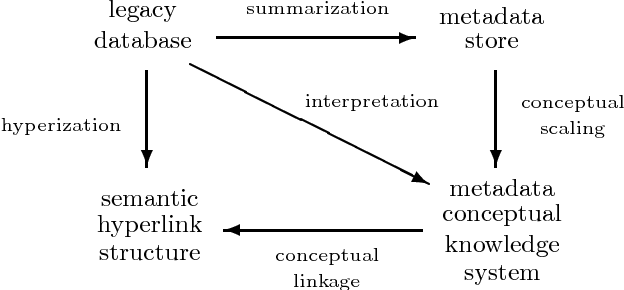
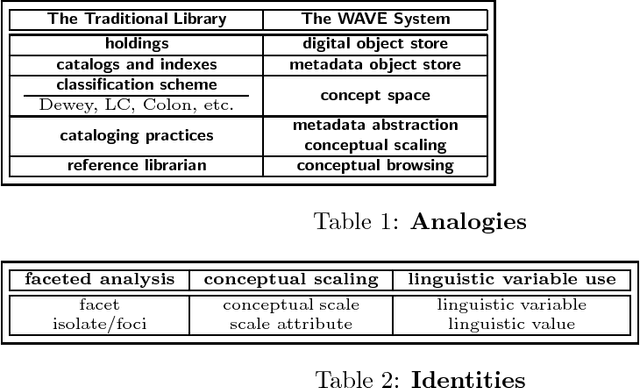
Conceptual Analysis of Hypertext

In this chapter tools and techniques from the mathematical theory of formal concept analysis are applied to hypertext systems in general, and the World Wide Web in particular. Various processes for the conceptual structuring of hypertext are discussed: summarization, conceptual scaling, and the creation of conceptual links. Well-known interchange formats for summarizing networked information resources as resource meta-information are reviewed, and two new interchange formats originating from formal concept analysis are advocated. Also reviewed is conceptual scaling, which provides a principled approach to the faceted analysis techniques in library science classification. The important notion of conceptual linkage is introduced as a generalization of a hyperlink. The automatic hyperization of the content of legacy data is described, and the composite conceptual structuring with hypertext linkage is defined. For the conceptual empowerment of the Web user, a new technique called conceptual browsing is advocated. Conceptual browsing, which browses over conceptual links, is dual mode (extensional versus intensional) and dual scope (global versus local).

Conceptual Collectives

The notions of formal contexts and concept lattices, although introduced by Wille only ten years ago, already have proven to be of great utility in various applications such as data analysis and knowledge representation. In this paper we give arguments that Wille's original notion of formal context, although quite appealing in its simplicity, now should be replaced by a more semantic notion. This new notion of formal context entails a modified approach to concept construction. We base our arguments for these new versions of formal context and concept construction upon Wille's philosophical attitude with reference to the intensional aspect of concepts. We give a brief development of the relational theory of formal contexts and concept construction, demonstrating the equivalence of "concept-lattice construction" of Wille with the well-known "completion by cuts" of MacNeille. Generalization and abstraction of these formal contexts offers a powerful approach to knowledge representation.

Formal Concept Analysis with Many-sorted Attributes

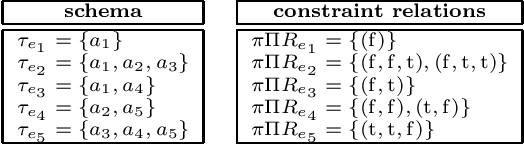
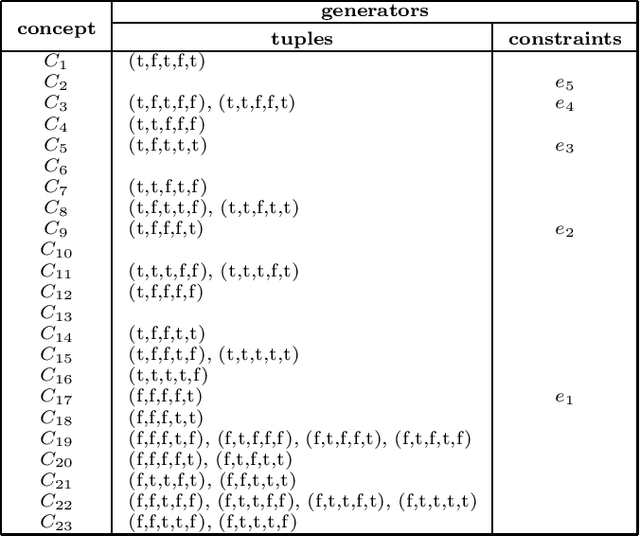
This paper unites two problem-solving traditions in computer science: (1) constraint-based reasoning, and (2) formal concept analysis. For basic definitions and properties of networks of constraints, we follow the foundational approach of Montanari and Rossi. This paper advocates distributed relations as a more semantic version of networks of constraints. The theory developed here uses the theory of formal concept analysis, pioneered by Rudolf Wille and his colleagues, as a key for unlocking the hidden semantic structure within distributed relations. Conversely, this paper offers distributed relations as a seamless many-sorted extension to the formal contexts of formal concept analysis. Some of the intuitions underlying our approach were discussed in a preliminary fashion by Freuder and Wallace.

Rough Concept Analysis

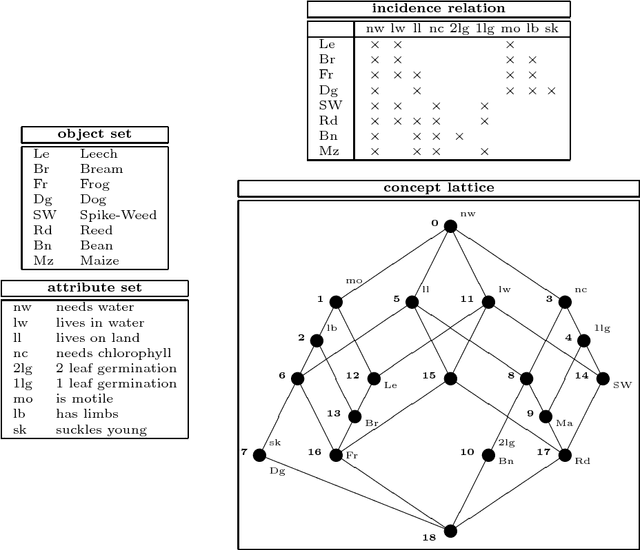
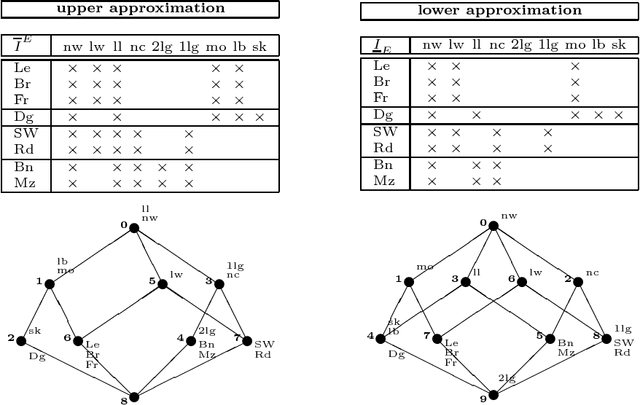
The theory introduced, presented and developed in this paper, is concerned with Rough Concept Analysis. This theory is a synthesis of the theory of Rough Sets pioneered by Zdzislaw Pawlak with the theory of Formal Concept Analysis pioneered by Rudolf Wille. The central notion in this paper of a rough formal concept combines in a natural fashion the notion of a rough set with the notion of a formal concept: "rough set + formal concept = rough formal concept". A follow-up paper will provide a synthesis of the two important data modeling techniques: conceptual scaling of Formal Concept Analysis and Entity-Relationship database modeling.

Conceptual Knowledge Markup Language: An Introduction

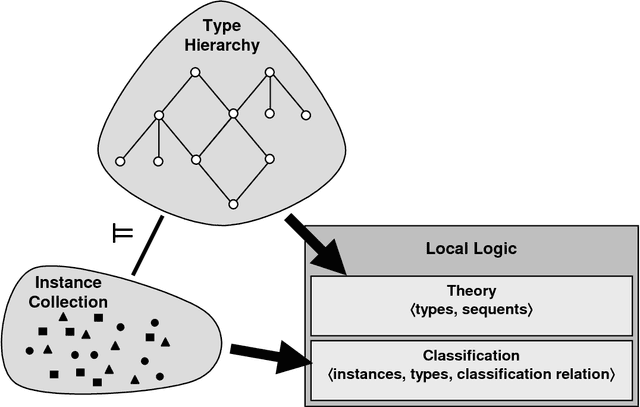
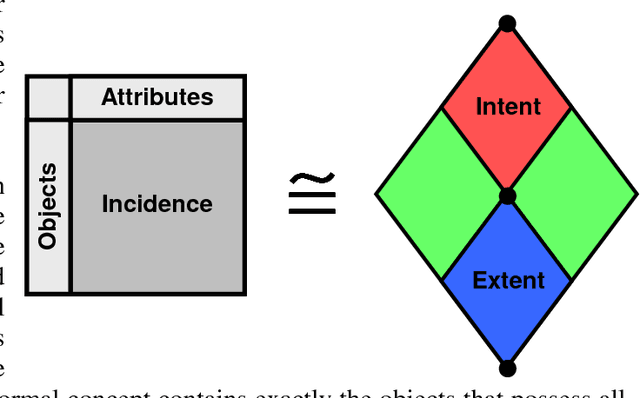
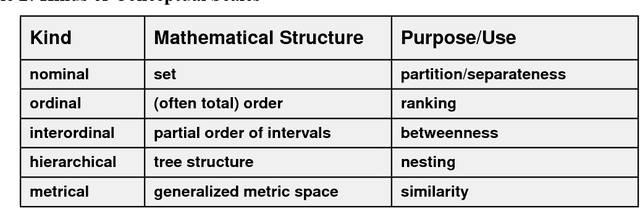
Conceptual Knowledge Markup Language (CKML) is an application of XML. Earlier versions of CKML followed rather exclusively the philosophy of Conceptual Knowledge Processing (CKP), a principled approach to knowledge representation and data analysis that "advocates methods and instruments of conceptual knowledge processing which support people in their rational thinking, judgment and acting and promote critical discussion." The new version of CKML continues to follow this approach, but also incorporates various principles, insights and techniques from Information Flow (IF), the logical design of distributed systems. Among other things, this allows diverse communities of discourse to compare their own information structures, as coded in logical theories, with that of other communities that share a common generic ontology. CKML incorporates the CKP ideas of concept lattice and formal context, along with the IF ideas of classification (= formal context), infomorphism, theory, interpretation and local logic. Ontology Markup Language (OML), a subset of CKML that is a self-sufficient markup language in its own right, follows the principles and ideas of Conceptual Graphs (CG). OML is used for structuring the specifications and axiomatics of metadata into ontologies. OML incorporates the CG ideas of concept, conceptual relation, conceptual graph, conceptual context, participants and ontology. The link from OML to CKML is the process of conceptual scaling, which is the interpretive transformation of ontologically structured knowledge to conceptual structured knowledge.