Soft Concept Analysis
Paper and Code
Oct 21, 2018
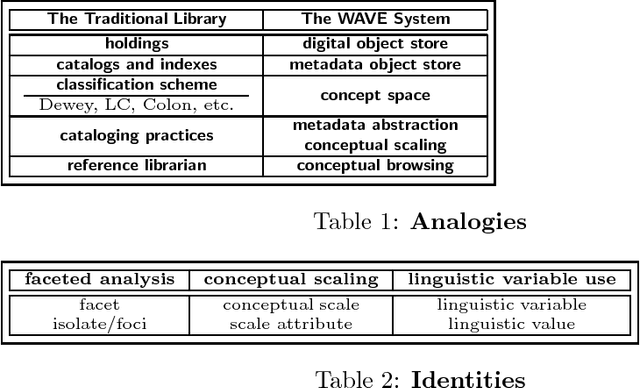
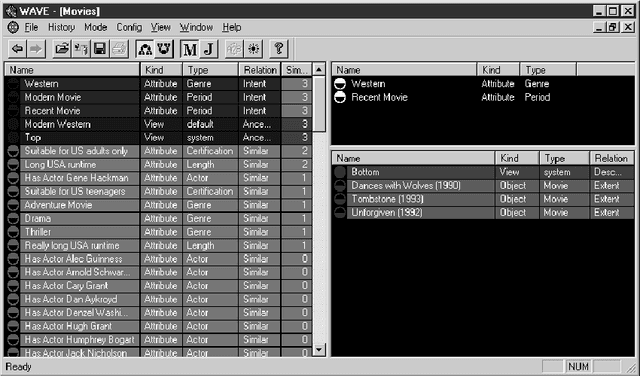

In this chapter we discuss soft concept analysis, a study which identifies an enriched notion of "conceptual scale" as developed in formal concept analysis with an enriched notion of "linguistic variable" as discussed in fuzzy logic. The identification "enriched conceptual scale" = "enriched linguistic variable" was made in a previous paper (Enriched interpretation, Robert E. Kent). In this chapter we offer further arguments for the importance of this identification by discussing the philosophy, spirit, and practical application of conceptual scaling to the discovery, conceptual analysis, interpretation, and categorization of networked information resources. We argue that a linguistic variable, which has been defined at just the right generalization of valuated categories, provides a natural definition for the process of soft conceptual scaling. This enrichment using valuated categories models the relation of indiscernability, a notion of central importance in rough set theory. At a more fundamental level for soft concept analysis, it also models the derivation of formal concepts, a process of central importance in formal concept analysis. Soft concept analysis is synonymous with enriched concept analysis. From one viewpoint, the study of soft concept analysis that is initiated here extends formal concept analysis to soft computational structures. From another viewpoint, soft concept analysis provides a natural foundation for soft computation by unifying and explaining notions from soft computation in terms of suitably generalized notions from formal concept analysis, rough set theory and fuzzy set theory.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge