Linear Quadratic Guidance Law for Joint Motion Planning of a Pursuer-Turret Assembly

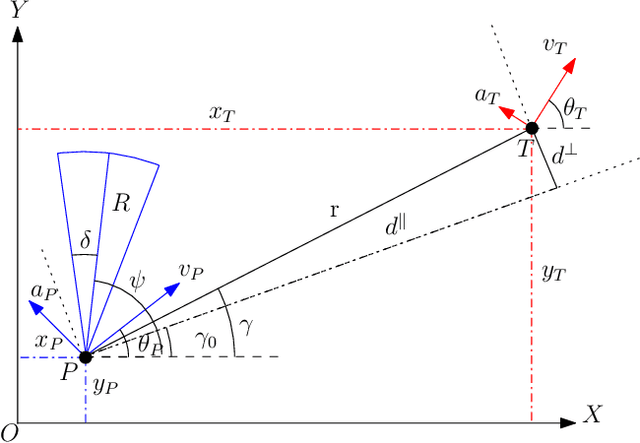
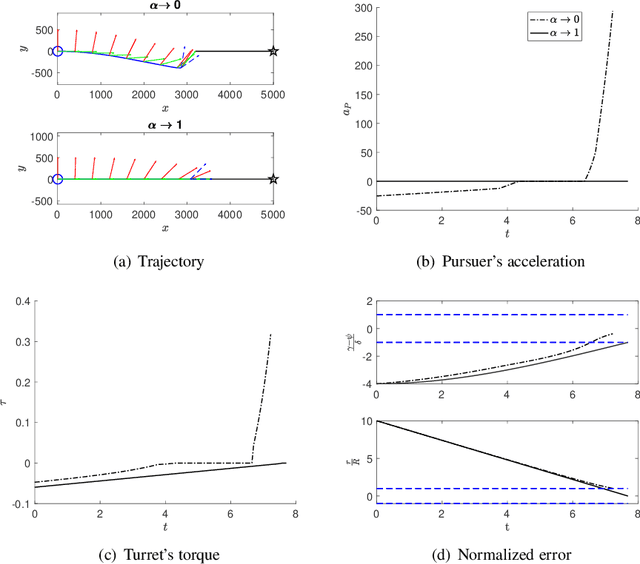
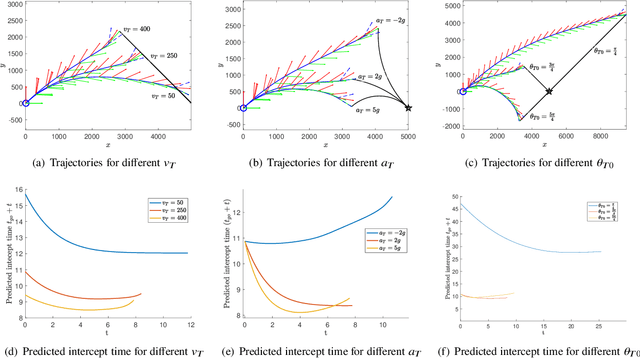
This paper presents joint motion planning of a vehicle with an attached rotating turret. The turret has a limited range as well as the field of view. The objective is capture a maneuvering target such that at the terminal time it is withing the field-of-view and range limits. Catering to it, we present a minimum effort guidance law that commensurate for the turn rate abilities of the vehicle and the turret. The guidance law is obtained using linearization about the collision triangle and admits an analytical solution. Simulation results are presented to exemplify the cooperation between the turret and the vehicle.

The Weighted Markov-Dubins Problem

In this article, a variation of the classical Markov-Dubins problem is considered, which deals with curvature-constrained least-cost paths in a plane with prescribed initial and final configurations, different bounds for the sinistral and dextral curvatures, and penalties $\mu_L$ and $\mu_R$ for the sinistral and dextral turns, respectively. The addressed problem generalizes the classical Markov-Dubins problem and the asymmetric sinistral/dextral Markov-Dubins problem. The proposed formulation can be used to model an Unmanned Aerial Vehicle (UAV) with a penalty associated with a turn due to a loss in altitude while turning or a UAV with different costs for the sinistral and dextral turns due to hardware failures or environmental conditions. Using optimal control theory, the main result of this paper shows that the optimal path belongs to a set of at most $21$ candidate paths, each comprising of at most five segments. Unlike in the classical Markov-Dubins problem, the $CCC$ path, which is a candidate path for the classical Markov-Dubins problem, is not optimal for the weighted Markov-Dubins problem. Moreover, the obtained list of candidate paths for the weighted Markov-Dubins problem reduces to the standard $CSC$ and $CCC$ paths and the corresponding degenerate paths when $\mu_L$ and $\mu_R$ approach zero.

Bounds on Optimal Revisit Times in Persistent Monitoring Missions with a Distinct \& Remote Service Station

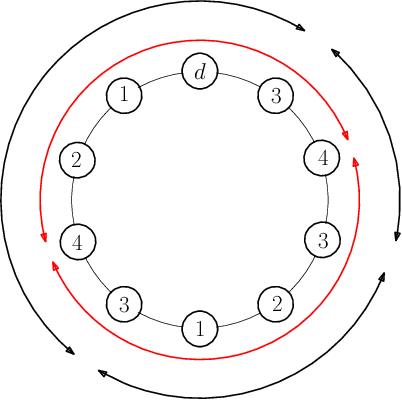
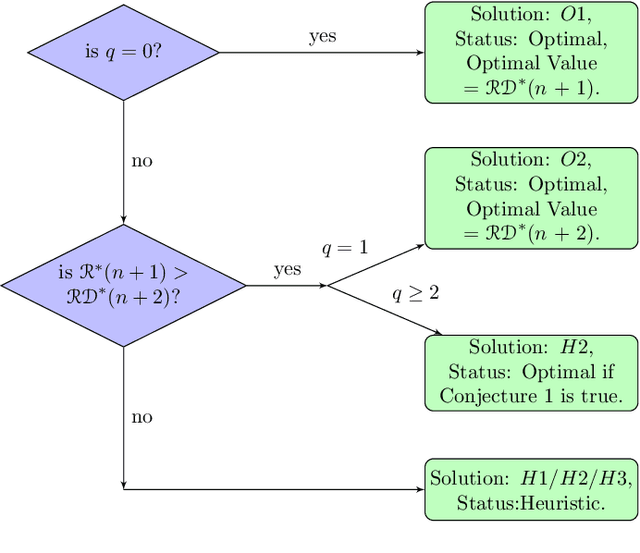
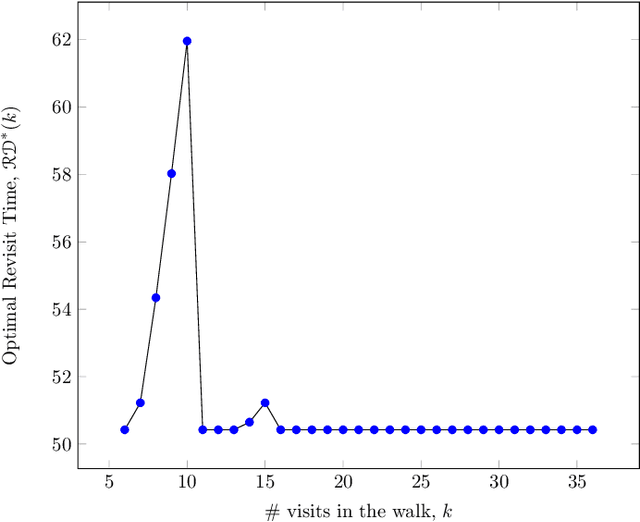
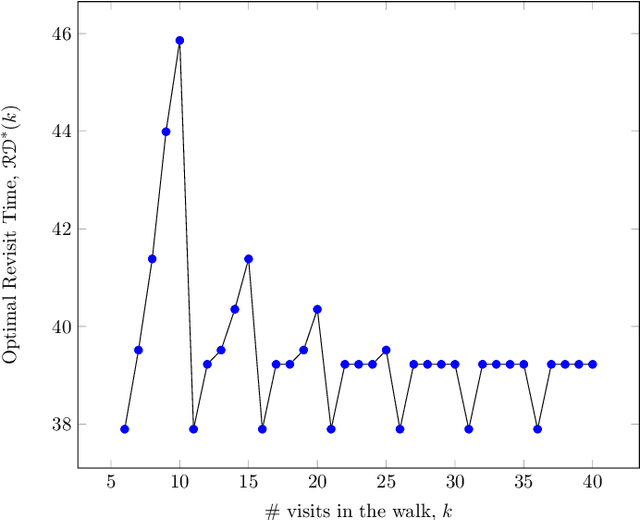
Persistent monitoring missions require an up-to-date knowledge of the changing state of the underlying environment. UAVs can be gainfully employed to continually visit a set of targets representing tasks (and locations) in the environment and collect data therein for long time periods. The enduring nature of these missions requires the UAV to be regularly recharged at a service station. In this paper, we consider the case in which the service station is not co-located with any of the targets. An efficient monitoring requires the revisit time, defined as the maximum of the time elapsed between successive revisits to targets, to be minimized. Here, we consider the problem of determining UAV routes that lead to the minimum revisit time. The problem is NP-hard, and its computational difficulty increases with the fuel capacity of the UAV. We develop an algorithm to construct near-optimal solutions to the problem quickly, when the fuel capacity exceeds a threshold. We also develop lower bounds to the optimal revisit time and use these bounds to demonstrate (through numerical simulations) that the constructed solutions are, on an average, at most 0.01% away from the optimum.

Persistent Monitoring of Dynamically Changing Environments Using an Unmanned Vehicle

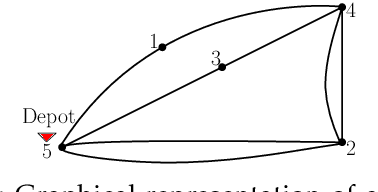
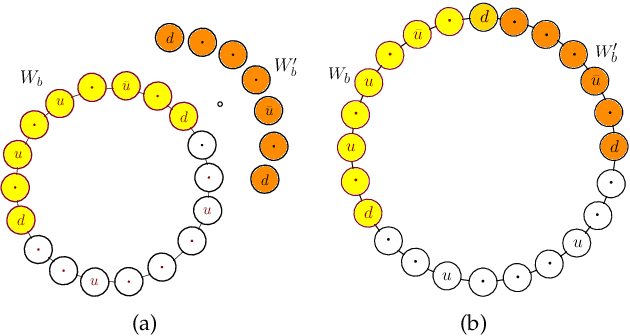
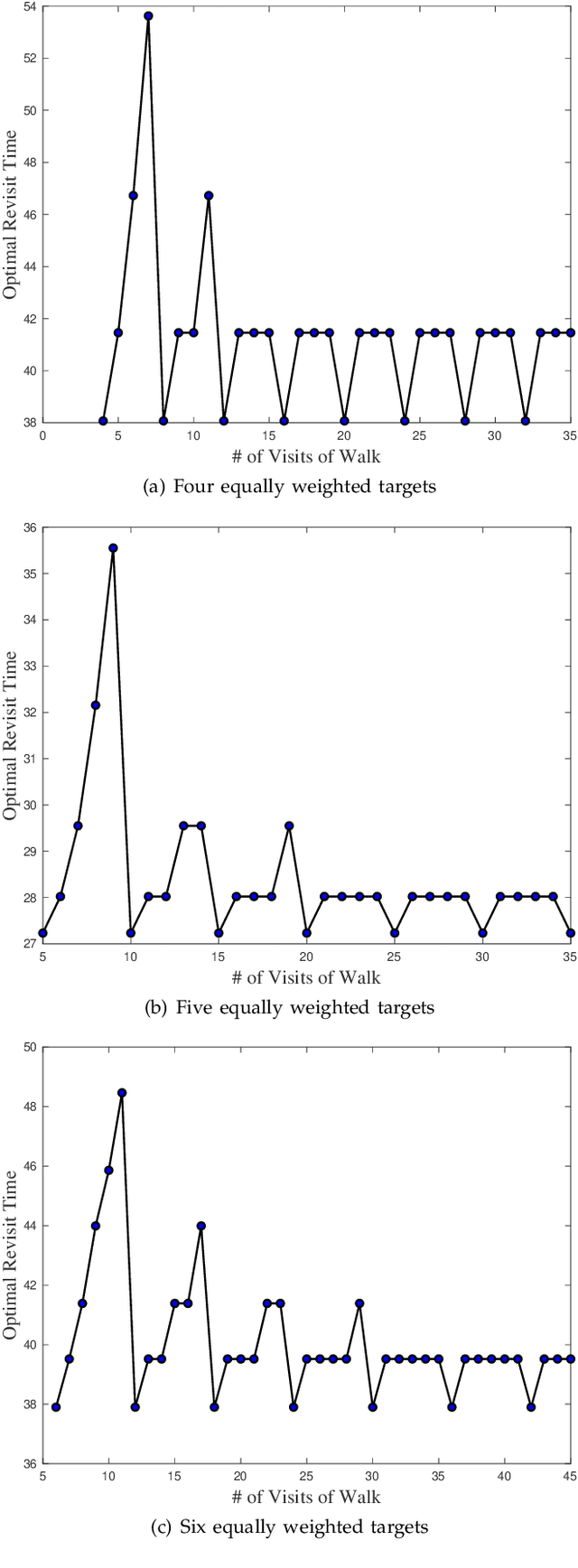
We consider the problem of planning a closed walk $\mathcal W$ for a UAV to persistently monitor a finite number of stationary targets with equal priorities and dynamically changing properties. A UAV must physically visit the targets in order to monitor them and collect information therein. The frequency of monitoring any given target is specified by a target revisit time, $i.e.$, the maximum allowable time between any two successive visits to the target. The problem considered in this paper is the following: Given $n$ targets and $k \geq n$ allowed visits to them, find an optimal closed walk $\mathcal W^*(k)$ so that every target is visited at least once and the maximum revisit time over all the targets, $\mathcal R(\mathcal W(k))$, is minimized. We prove the following: If $k \geq n^2-n$, $\mathcal R(\mathcal W^*(k))$ (or simply, $\mathcal R^*(k)$) takes only two values: $\mathcal R^*(n)$ when $k$ is an integral multiple of $n$, and $\mathcal R^*(n+1)$ otherwise. This result suggests significant computational savings - one only needs to determine $\mathcal W^*(n)$ and $\mathcal W^*(n+1)$ to construct an optimal solution $\mathcal W^*(k)$. We provide MILP formulations for computing $\mathcal W^*(n)$ and $\mathcal W^*(n+1)$. Furthermore, for {\it any} given $k$, we prove that $\mathcal R^*(k) \geq \mathcal R^*(k+n)$.

Shortest Paths of Bounded Curvature for the Dubins Interval Problem

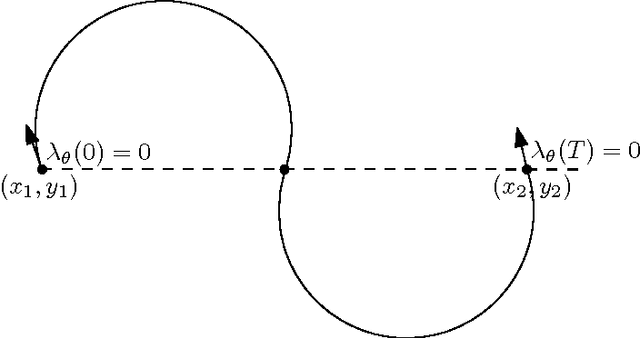
The Dubins interval problem aims to find the shortest path of bounded curvature between two targets such that the departure angle from the first target and the arrival angle at the second target are constrained to two respective intervals. We propose a new and a simple algorithm to this problem based on the minimum principle of Pontryagin.

Circumnavigation of an Unknown Target Using UAVs with Range and Range Rate Measurements

This paper presents two control algorithms enabling a UAV to circumnavigate an unknown target using range and range rate (i.e., the derivative of range) measurements. Given a prescribed orbit radius, both control algorithms (i) tend to drive the UAV toward the tangent of prescribed orbit when the UAV is outside or on the orbit, and (ii) apply zero control input if the UAV is inside the desired orbit. The algorithms differ in that, the first algorithm is smooth and unsaturated while the second algorithm is non-smooth and saturated. By analyzing properties associated with the bearing angle of the UAV relative to the target and through proper design of Lyapunov functions, it is shown that both algorithms produce the desired orbit for an arbitrary initial state. Three examples are provided as a proof of concept.