Persistent Monitoring of Dynamically Changing Environments Using an Unmanned Vehicle
Paper and Code
Aug 07, 2018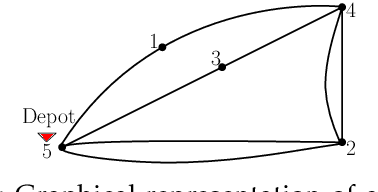
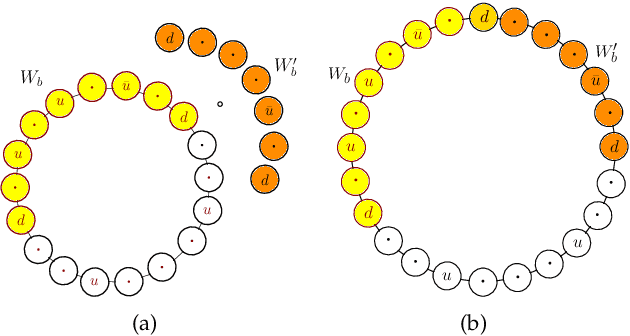
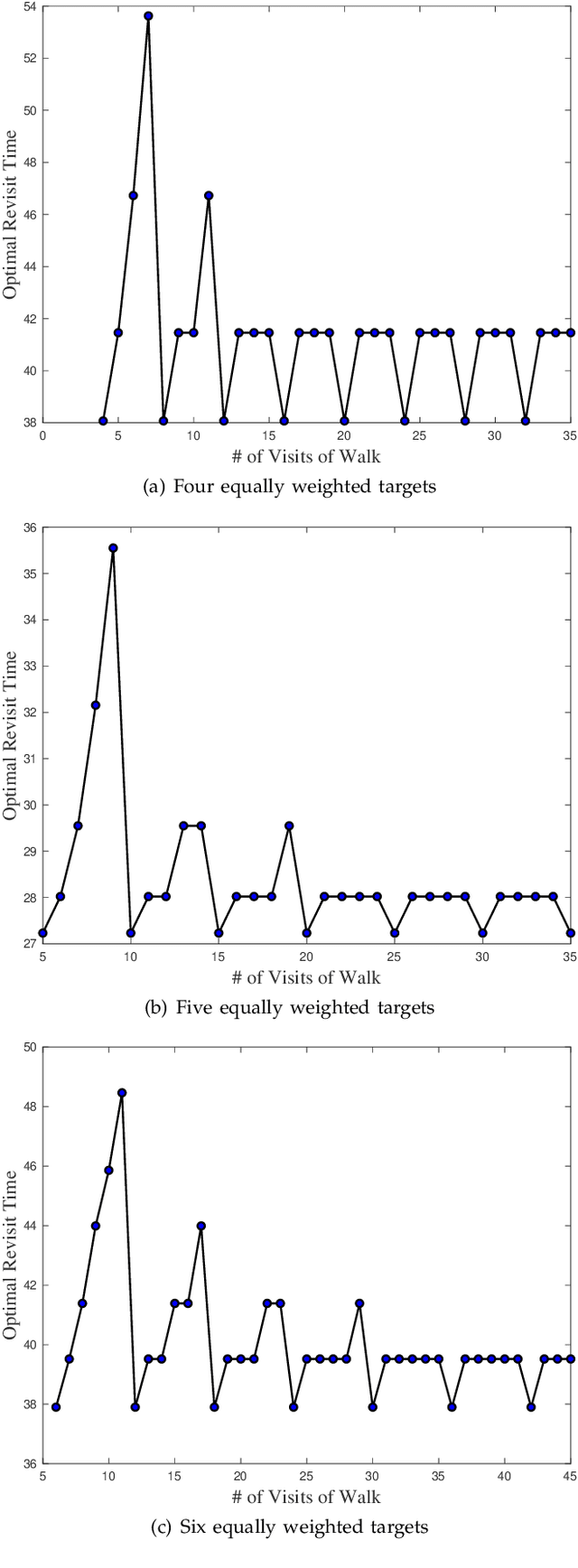
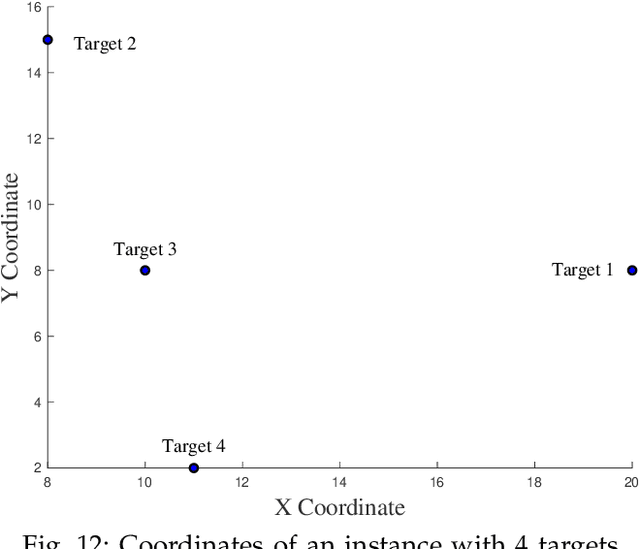
We consider the problem of planning a closed walk $\mathcal W$ for a UAV to persistently monitor a finite number of stationary targets with equal priorities and dynamically changing properties. A UAV must physically visit the targets in order to monitor them and collect information therein. The frequency of monitoring any given target is specified by a target revisit time, $i.e.$, the maximum allowable time between any two successive visits to the target. The problem considered in this paper is the following: Given $n$ targets and $k \geq n$ allowed visits to them, find an optimal closed walk $\mathcal W^*(k)$ so that every target is visited at least once and the maximum revisit time over all the targets, $\mathcal R(\mathcal W(k))$, is minimized. We prove the following: If $k \geq n^2-n$, $\mathcal R(\mathcal W^*(k))$ (or simply, $\mathcal R^*(k)$) takes only two values: $\mathcal R^*(n)$ when $k$ is an integral multiple of $n$, and $\mathcal R^*(n+1)$ otherwise. This result suggests significant computational savings - one only needs to determine $\mathcal W^*(n)$ and $\mathcal W^*(n+1)$ to construct an optimal solution $\mathcal W^*(k)$. We provide MILP formulations for computing $\mathcal W^*(n)$ and $\mathcal W^*(n+1)$. Furthermore, for {\it any} given $k$, we prove that $\mathcal R^*(k) \geq \mathcal R^*(k+n)$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge