The Weighted Markov-Dubins Problem

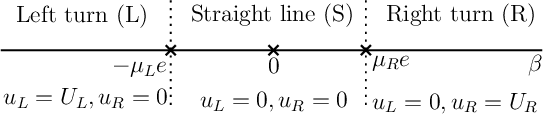
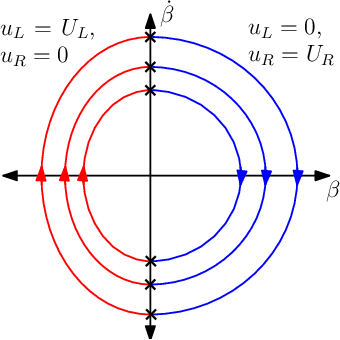
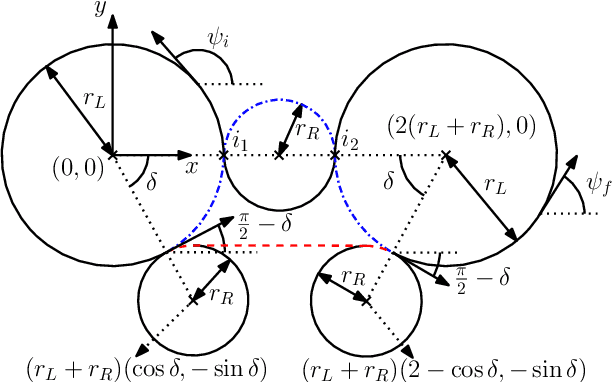
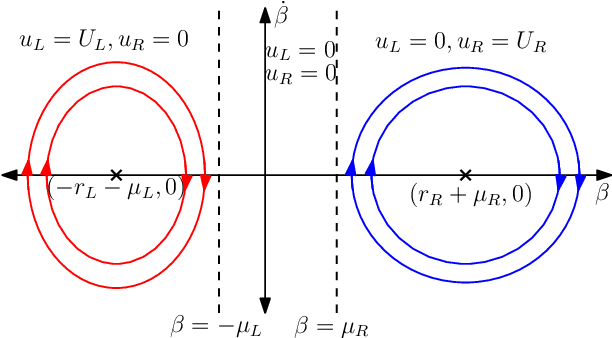
In this article, a variation of the classical Markov-Dubins problem is considered, which deals with curvature-constrained least-cost paths in a plane with prescribed initial and final configurations, different bounds for the sinistral and dextral curvatures, and penalties $\mu_L$ and $\mu_R$ for the sinistral and dextral turns, respectively. The addressed problem generalizes the classical Markov-Dubins problem and the asymmetric sinistral/dextral Markov-Dubins problem. The proposed formulation can be used to model an Unmanned Aerial Vehicle (UAV) with a penalty associated with a turn due to a loss in altitude while turning or a UAV with different costs for the sinistral and dextral turns due to hardware failures or environmental conditions. Using optimal control theory, the main result of this paper shows that the optimal path belongs to a set of at most $21$ candidate paths, each comprising of at most five segments. Unlike in the classical Markov-Dubins problem, the $CCC$ path, which is a candidate path for the classical Markov-Dubins problem, is not optimal for the weighted Markov-Dubins problem. Moreover, the obtained list of candidate paths for the weighted Markov-Dubins problem reduces to the standard $CSC$ and $CCC$ paths and the corresponding degenerate paths when $\mu_L$ and $\mu_R$ approach zero.

Bounds on Optimal Revisit Times in Persistent Monitoring Missions with a Distinct \& Remote Service Station

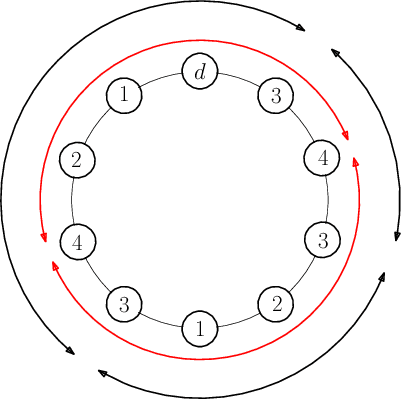
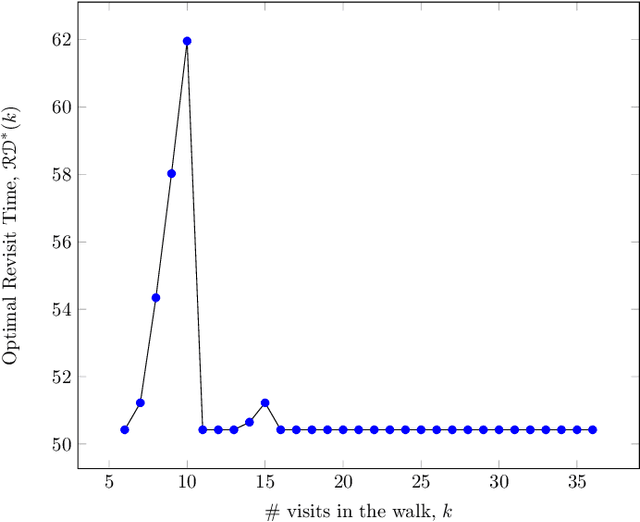
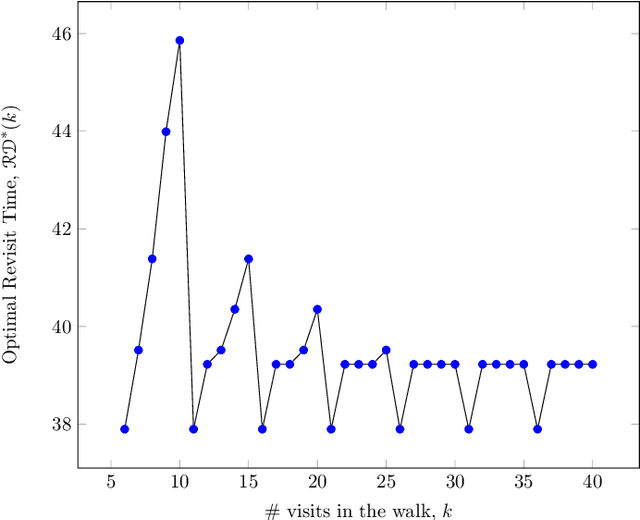
Persistent monitoring missions require an up-to-date knowledge of the changing state of the underlying environment. UAVs can be gainfully employed to continually visit a set of targets representing tasks (and locations) in the environment and collect data therein for long time periods. The enduring nature of these missions requires the UAV to be regularly recharged at a service station. In this paper, we consider the case in which the service station is not co-located with any of the targets. An efficient monitoring requires the revisit time, defined as the maximum of the time elapsed between successive revisits to targets, to be minimized. Here, we consider the problem of determining UAV routes that lead to the minimum revisit time. The problem is NP-hard, and its computational difficulty increases with the fuel capacity of the UAV. We develop an algorithm to construct near-optimal solutions to the problem quickly, when the fuel capacity exceeds a threshold. We also develop lower bounds to the optimal revisit time and use these bounds to demonstrate (through numerical simulations) that the constructed solutions are, on an average, at most 0.01% away from the optimum.

Path Planning Algorithms for a Car-Like Robot visiting a set of Waypoints with Field of View Constraints

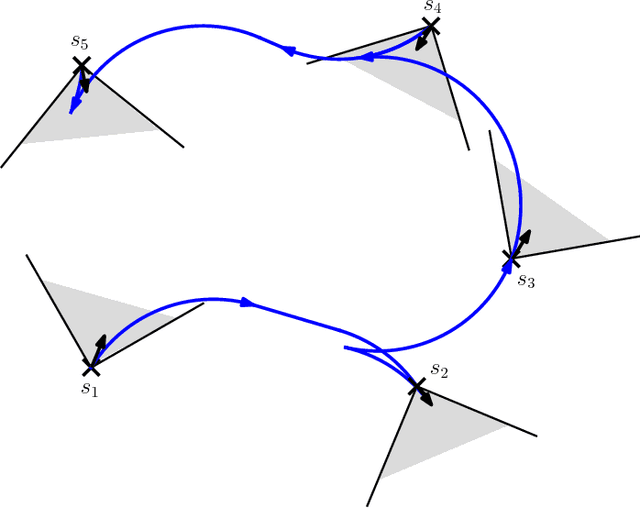
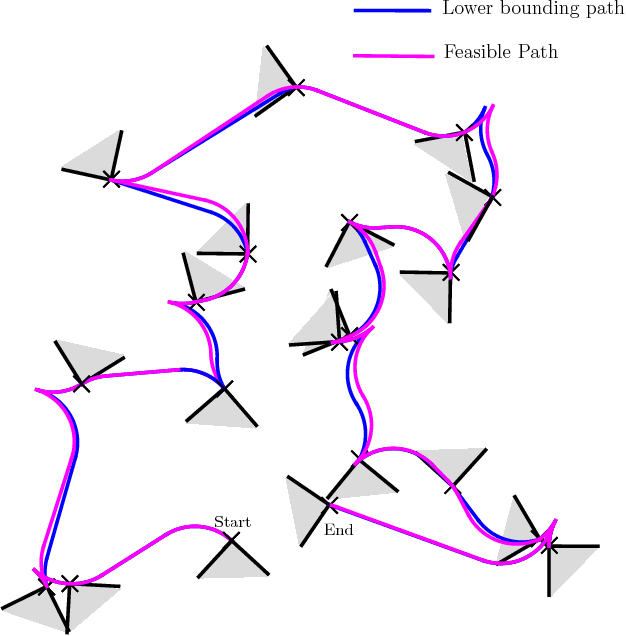
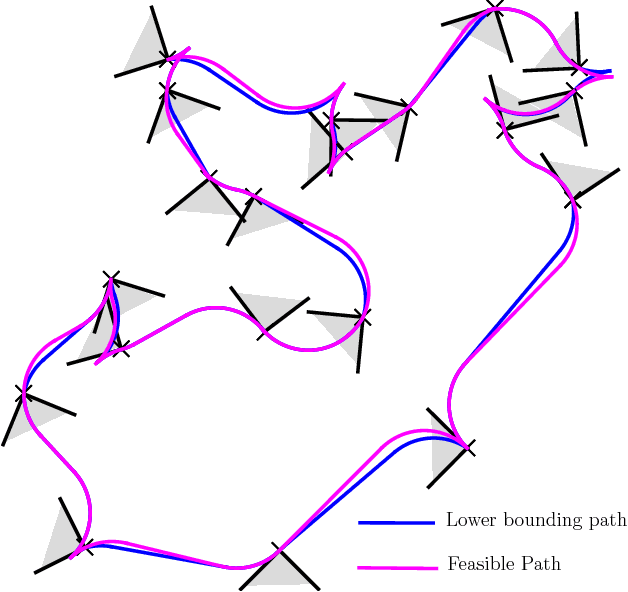
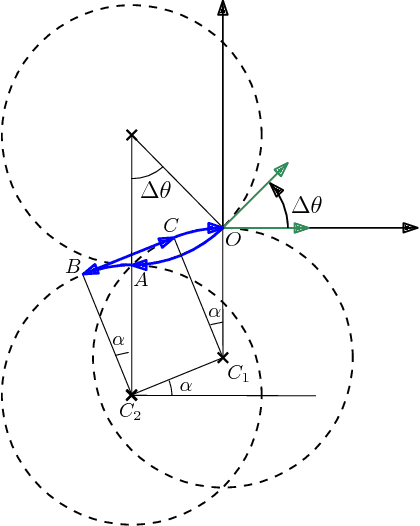
This article considers two variants of a shortest path problem for a car-like robot visiting a set of waypoints. The sequence of waypoints to be visited is specified in the first variant while the robot is allowed to visit the waypoints in any sequence in the second variant. Field of view constraints are also placed when the robot arrives at a waypoint, i.e., the orientation of the robot at any waypoint is restricted to belong to a given interval of angles at the waypoint. The shortest path problem is first solved for two waypoints with the field of view constraints using Pontryagin's minimum principle. Using the results for the two point problem, tight lower and upper bounds on the length of the shortest path are developed for visiting n points by relaxing the requirement that the arrival angle must be equal to the departure angle of the robot at each waypoint. Theoretical bounds are also provided on the length of the feasible solutions obtained by the proposed algorithm. Simulation results verify the performance of the bounds for instances with 20 waypoints.

Persistent Monitoring of Dynamically Changing Environments Using an Unmanned Vehicle

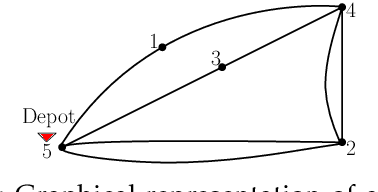
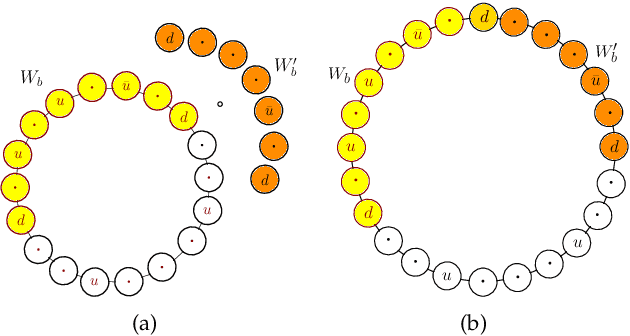
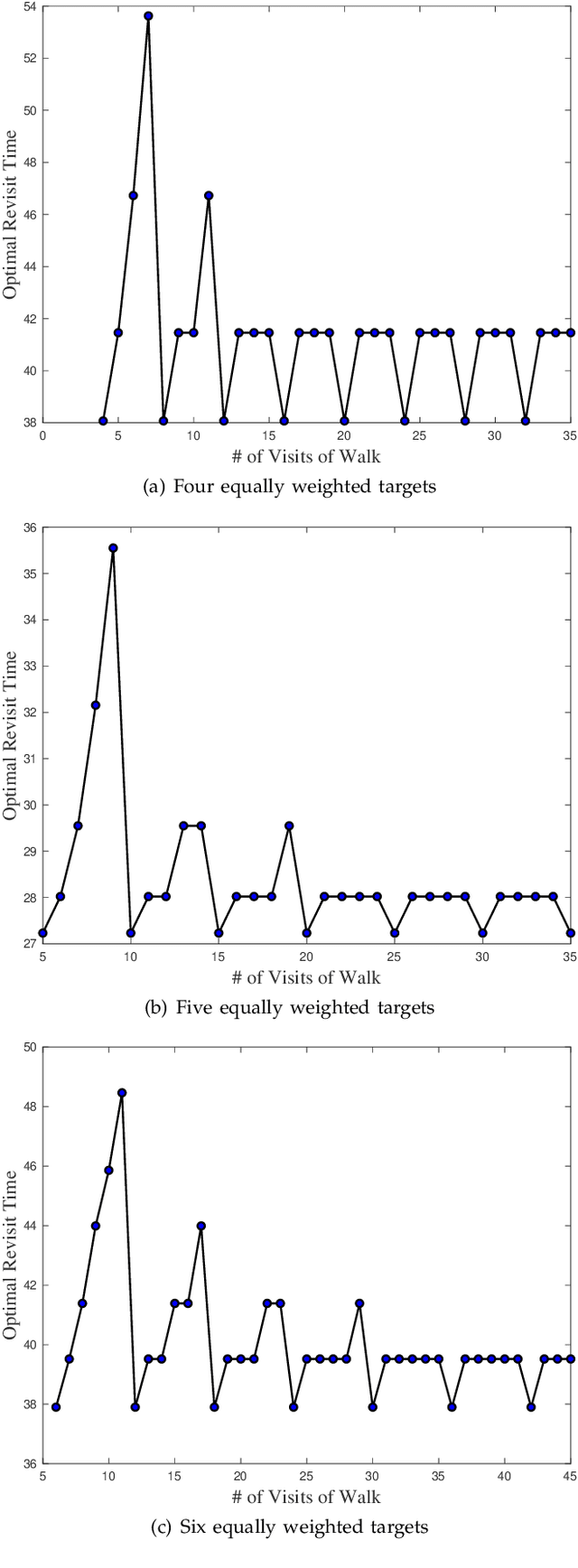
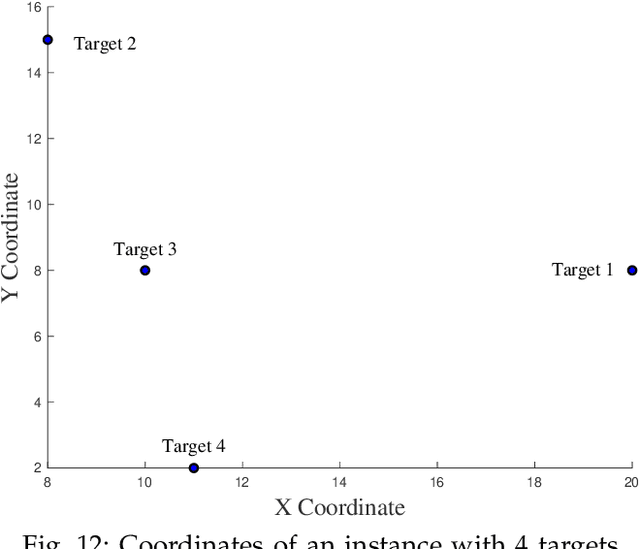
We consider the problem of planning a closed walk $\mathcal W$ for a UAV to persistently monitor a finite number of stationary targets with equal priorities and dynamically changing properties. A UAV must physically visit the targets in order to monitor them and collect information therein. The frequency of monitoring any given target is specified by a target revisit time, $i.e.$, the maximum allowable time between any two successive visits to the target. The problem considered in this paper is the following: Given $n$ targets and $k \geq n$ allowed visits to them, find an optimal closed walk $\mathcal W^*(k)$ so that every target is visited at least once and the maximum revisit time over all the targets, $\mathcal R(\mathcal W(k))$, is minimized. We prove the following: If $k \geq n^2-n$, $\mathcal R(\mathcal W^*(k))$ (or simply, $\mathcal R^*(k)$) takes only two values: $\mathcal R^*(n)$ when $k$ is an integral multiple of $n$, and $\mathcal R^*(n+1)$ otherwise. This result suggests significant computational savings - one only needs to determine $\mathcal W^*(n)$ and $\mathcal W^*(n+1)$ to construct an optimal solution $\mathcal W^*(k)$. We provide MILP formulations for computing $\mathcal W^*(n)$ and $\mathcal W^*(n+1)$. Furthermore, for {\it any} given $k$, we prove that $\mathcal R^*(k) \geq \mathcal R^*(k+n)$.