Yuntao Zhang
Wavelet Prior Attention Learning in Axial Inpainting Network
Jun 07, 2022

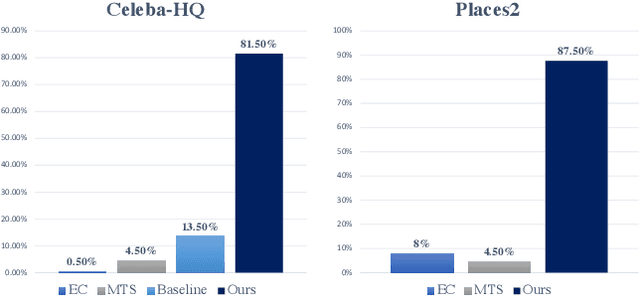
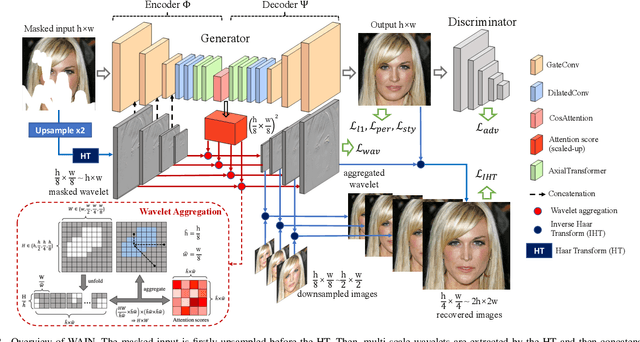
Abstract:Image inpainting is the task of filling masked or unknown regions of an image with visually realistic contents, which has been remarkably improved by Deep Neural Networks (DNNs) recently. Essentially, as an inverse problem, the inpainting has the underlying challenges of reconstructing semantically coherent results without texture artifacts. Many previous efforts have been made via exploiting attention mechanisms and prior knowledge, such as edges and semantic segmentation. However, these works are still limited in practice by an avalanche of learnable prior parameters and prohibitive computational burden. To this end, we propose a novel model -- Wavelet prior attention learning in Axial Inpainting Network (WAIN), whose generator contains the encoder, decoder, as well as two key components of Wavelet image Prior Attention (WPA) and stacked multi-layer Axial-Transformers (ATs). Particularly, the WPA guides the high-level feature aggregation in the multi-scale frequency domain, alleviating the textual artifacts. Stacked ATs employ unmasked clues to help model reasonable features along with low-level features of horizontal and vertical axes, improving the semantic coherence. Extensive quantitative and qualitative experiments on Celeba-HQ and Places2 datasets are conducted to validate that our WAIN can achieve state-of-the-art performance over the competitors. The codes and models will be released.
Path Planning Algorithms for a Car-Like Robot visiting a set of Waypoints with Field of View Constraints
Sep 11, 2018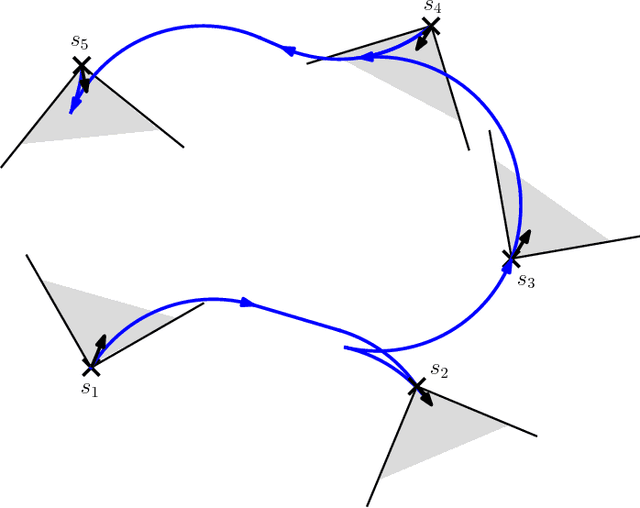
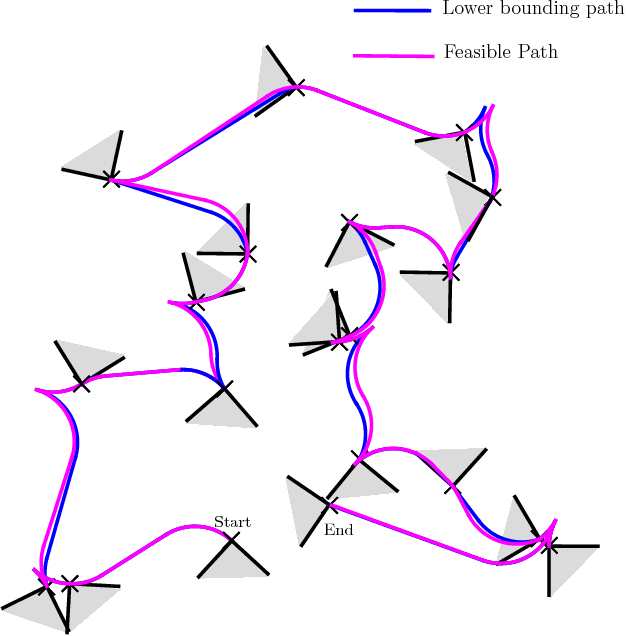
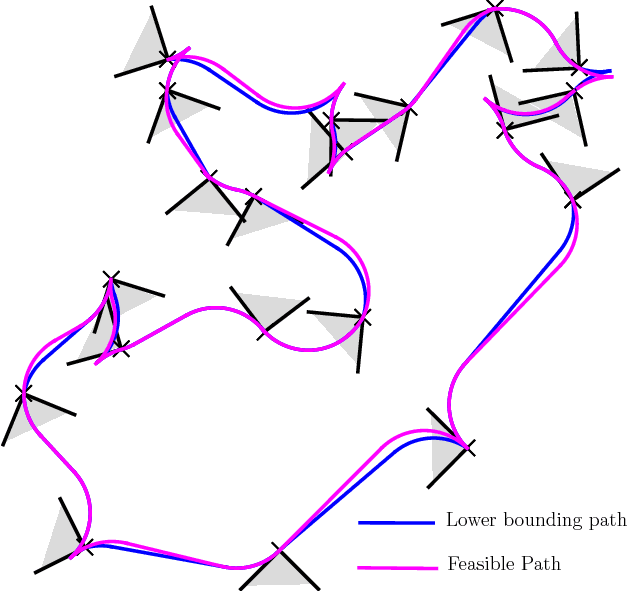
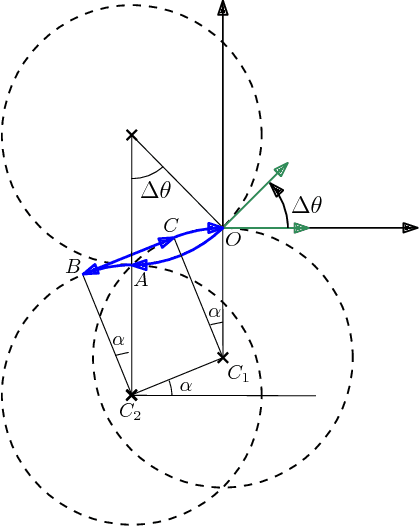
Abstract:This article considers two variants of a shortest path problem for a car-like robot visiting a set of waypoints. The sequence of waypoints to be visited is specified in the first variant while the robot is allowed to visit the waypoints in any sequence in the second variant. Field of view constraints are also placed when the robot arrives at a waypoint, i.e., the orientation of the robot at any waypoint is restricted to belong to a given interval of angles at the waypoint. The shortest path problem is first solved for two waypoints with the field of view constraints using Pontryagin's minimum principle. Using the results for the two point problem, tight lower and upper bounds on the length of the shortest path are developed for visiting n points by relaxing the requirement that the arrival angle must be equal to the departure angle of the robot at each waypoint. Theoretical bounds are also provided on the length of the feasible solutions obtained by the proposed algorithm. Simulation results verify the performance of the bounds for instances with 20 waypoints.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge