On Tightly Bounding the Dubins Traveling Salesman's Optimum

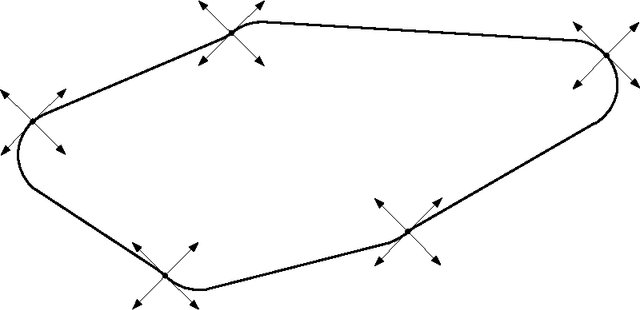
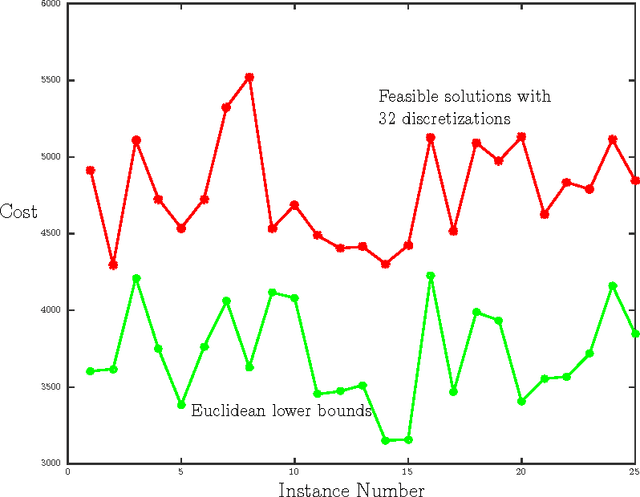
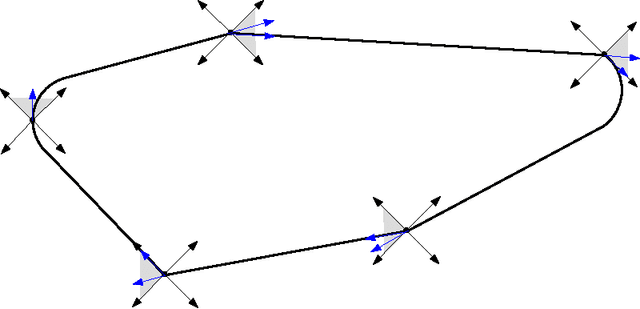
The Dubins Traveling Salesman Problem (DTSP) has generated significant interest over the last decade due to its occurrence in several civil and military surveillance applications. Currently, there is no algorithm that can find an optimal solution to the problem. In addition, relaxing the motion constraints and solving the resulting Euclidean TSP (ETSP) provides the only lower bound available for the problem. However, in many problem instances, the lower bound computed by solving the ETSP is far below the cost of the feasible solutions obtained by some well-known algorithms for the DTSP. This article addresses this fundamental issue and presents the first systematic procedure for developing tight lower bounds for the DTSP.

Shortest Paths of Bounded Curvature for the Dubins Interval Problem

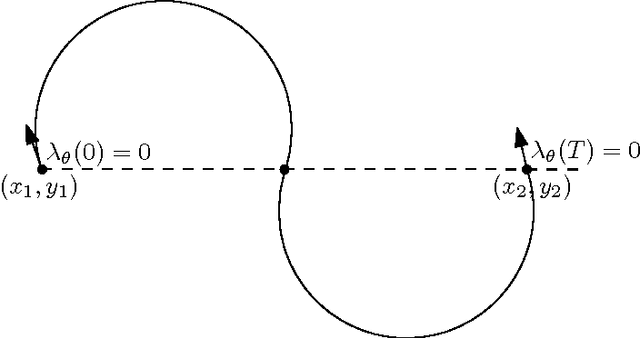
The Dubins interval problem aims to find the shortest path of bounded curvature between two targets such that the departure angle from the first target and the arrival angle at the second target are constrained to two respective intervals. We propose a new and a simple algorithm to this problem based on the minimum principle of Pontryagin.