Characterizing bearing equivalence in directed graphs

In this paper, we study bearing equivalence in directed graphs. We first give a strengthened definition of bearing equivalence based on the \textit{kernel equivalence} relationship between bearing rigidity matrix and bearing Laplacian matrix. We then present several conditions to characterize bearing equivalence for both directed acyclic and cyclic graphs. These conditions involve the spectrum and null space of the associated bearing Laplacian matrix for a directed bearing formation. For directed acyclic graphs, all eigenvalues of the associated bearing Laplacian are real and nonnegative, while for directed graphs containing cycles, the bearing Laplacian can have eigenvalues with negative real parts. Several examples of bearing equivalent and bearing non-equivalent formations are given to illustrate these conditions.

Cooperative Manipulation via Internal Force Regulation: A Rigidity Theory Perspective

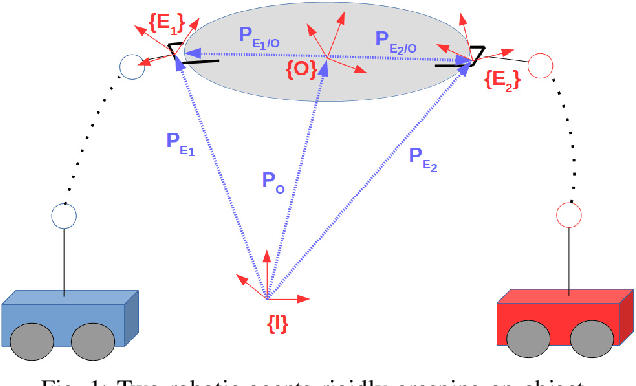
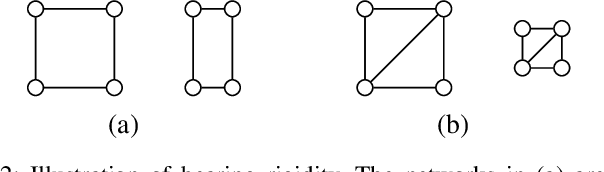
This paper considers the integration of rigid cooperative manipulation with rigidity theory. Motivated by rigid models of cooperative manipulation systems, i.e., where the grasping contacts are rigid, we introduce first the notion of bearing and distance rigidity for graph frameworks in SE(3). Next, we associate the nodes of these frameworks to the robotic agents of rigid cooperative manipulation schemes and we express the object-agent interaction forces by using the graph rigidity matrix, which encodes the infinitesimal rigid body motions of the system. Moreover, we show that the associated cooperative manipulation grasp matrix is related to the rigidity matrix via a range-nullspace relation, based on which we provide novel results on the relation between the arising interaction and internal forces and consequently on the energy-optimal force distribution on a cooperative manipulation system. Finally, simulation results on a realistic environment enhance the validity of the theoretical findings.

Decentralized Rigidity Maintenance Control with Range Measurements for Multi-Robot Systems

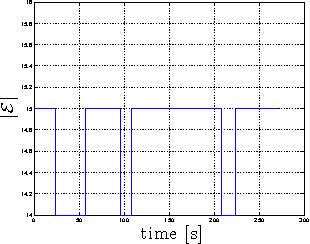
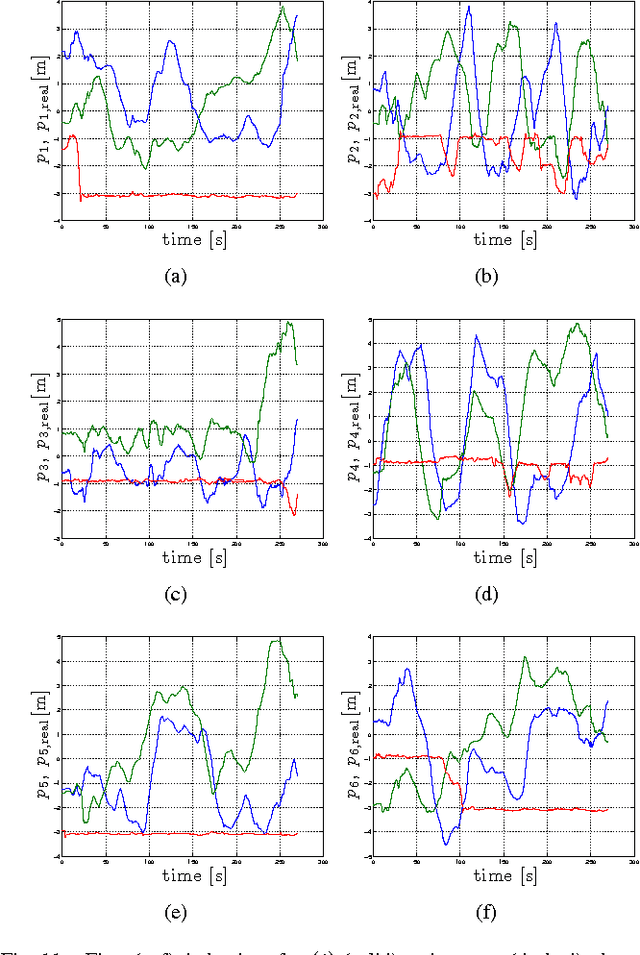
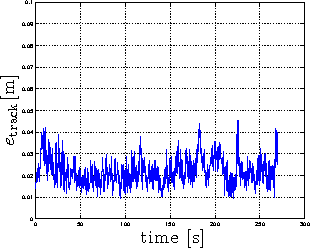
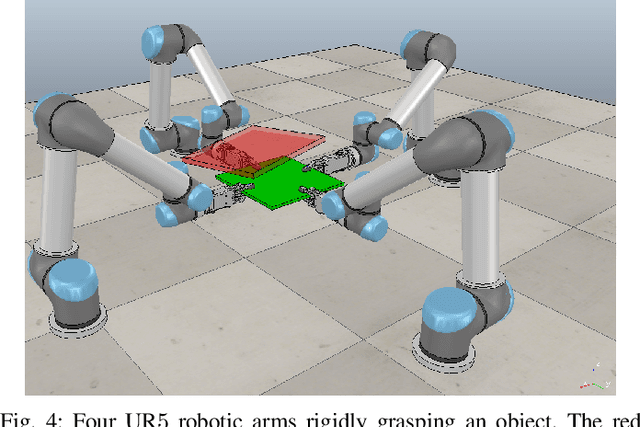
This work proposes a fully decentralized strategy for maintaining the formation rigidity of a multi-robot system using only range measurements, while still allowing the graph topology to change freely over time. In this direction, a first contribution of this work is an extension of rigidity theory to weighted frameworks and the rigidity eigenvalue, which when positive ensures the infinitesimal rigidity of the framework. We then propose a distributed algorithm for estimating a common relative position reference frame amongst a team of robots with only range measurements in addition to one agent endowed with the capability of measuring the bearing to two other agents. This first estimation step is embedded into a subsequent distributed algorithm for estimating the rigidity eigenvalue associated with the weighted framework. The estimate of the rigidity eigenvalue is finally used to generate a local control action for each agent that both maintains the rigidity property and enforces additional con- straints such as collision avoidance and sensing/communication range limits and occlusions. As an additional feature of our approach, the communication and sensing links among the robots are also left free to change over time while preserving rigidity of the whole framework. The proposed scheme is then experimentally validated with a robotic testbed consisting of 6 quadrotor UAVs operating in a cluttered environment.