Cooperative Manipulation via Internal Force Regulation: A Rigidity Theory Perspective
Paper and Code
Nov 04, 2019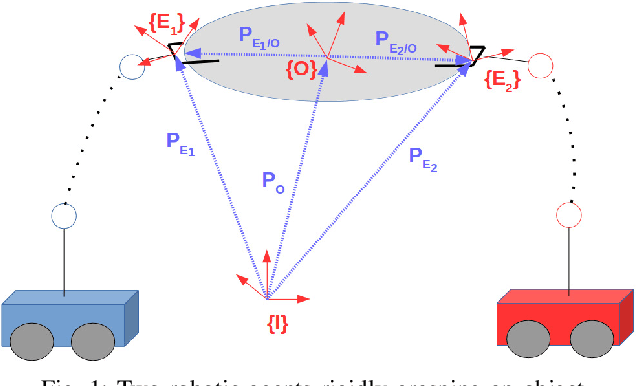
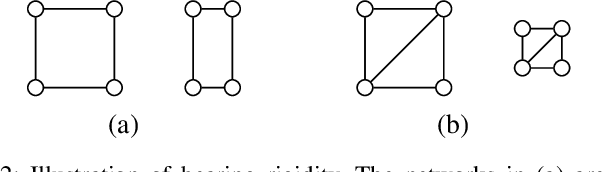

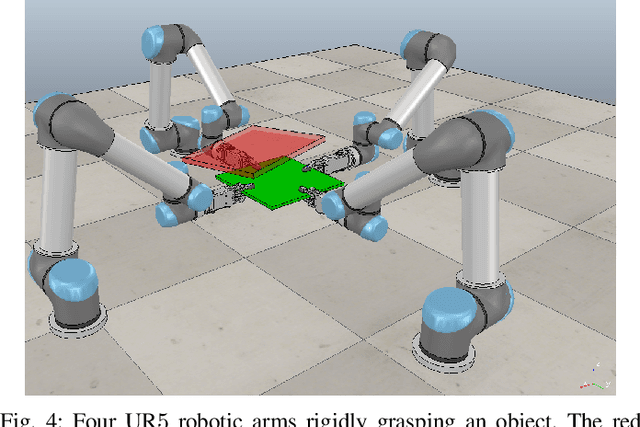
This paper considers the integration of rigid cooperative manipulation with rigidity theory. Motivated by rigid models of cooperative manipulation systems, i.e., where the grasping contacts are rigid, we introduce first the notion of bearing and distance rigidity for graph frameworks in SE(3). Next, we associate the nodes of these frameworks to the robotic agents of rigid cooperative manipulation schemes and we express the object-agent interaction forces by using the graph rigidity matrix, which encodes the infinitesimal rigid body motions of the system. Moreover, we show that the associated cooperative manipulation grasp matrix is related to the rigidity matrix via a range-nullspace relation, based on which we provide novel results on the relation between the arising interaction and internal forces and consequently on the energy-optimal force distribution on a cooperative manipulation system. Finally, simulation results on a realistic environment enhance the validity of the theoretical findings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge