The Deep Latent Space Particle Filter for Real-Time Data Assimilation with Uncertainty Quantification

In Data Assimilation, observations are fused with simulations to obtain an accurate estimate of the state and parameters for a given physical system. Combining data with a model, however, while accurately estimating uncertainty, is computationally expensive and infeasible to run in real-time for complex systems. Here, we present a novel particle filter methodology, the Deep Latent Space Particle filter or D-LSPF, that uses neural network-based surrogate models to overcome this computational challenge. The D-LSPF enables filtering in the low-dimensional latent space obtained using Wasserstein AEs with modified vision transformer layers for dimensionality reduction and transformers for parameterized latent space time stepping. As we demonstrate on three test cases, including leak localization in multi-phase pipe flow and seabed identification for fully nonlinear water waves, the D-LSPF runs orders of magnitude faster than a high-fidelity particle filter and 3-5 times faster than alternative methods while being up to an order of magnitude more accurate. The D-LSPF thus enables real-time data assimilation with uncertainty quantification for physical systems.

AIDA: Analytic Isolation and Distance-based Anomaly Detection Algorithm

We combine the metrics of distance and isolation to develop the Analytic Isolation and Distance-based Anomaly (AIDA) detection algorithm. AIDA is the first distance-based method that does not rely on the concept of nearest-neighbours, making it a parameter-free model. Differently from the prevailing literature, in which the isolation metric is always computed via simulations, we show that AIDA admits an analytical expression for the outlier score, providing new insights into the isolation metric. Additionally, we present an anomaly explanation method based on AIDA, the Tempered Isolation-based eXplanation (TIX) algorithm, which finds the most relevant outlier features even in data sets with hundreds of dimensions. We test both algorithms on synthetic and empirical data: we show that AIDA is competitive when compared to other state-of-the-art methods, and it is superior in finding outliers hidden in multidimensional feature subspaces. Finally, we illustrate how the TIX algorithm is able to find outliers in multidimensional feature subspaces, and use these explanations to analyze common benchmarks used in anomaly detection.

Convergence of a robust deep FBSDE method for stochastic control

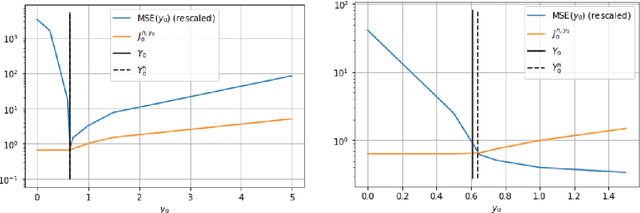
In this paper we propose a deep learning based numerical scheme for strongly coupled FBSDE, stemming from stochastic control. It is a modification of the deep BSDE method in which the initial value to the backward equation is not a free parameter, and with a new loss function being the weighted sum of the cost of the control problem, and a variance term which coincides with the means square error in the terminal condition. We show by a numerical example that a direct extension of the classical deep BSDE method to FBSDE, fails for a simple linear-quadratic control problem, and motivate why the new method works. Under regularity and boundedness assumptions on the exact controls of time continuous and time discrete control problems we provide an error analysis for our method. We show empirically that the method converges for three different problems, one being the one that failed for a direct extension of the deep BSDE method.

Monte Carlo Simulation of SDEs using GANs

Generative adversarial networks (GANs) have shown promising results when applied on partial differential equations and financial time series generation. We investigate if GANs can also be used to approximate one-dimensional Ito stochastic differential equations (SDEs). We propose a scheme that approximates the path-wise conditional distribution of SDEs for large time steps. Standard GANs are only able to approximate processes in distribution, yielding a weak approximation to the SDE. A conditional GAN architecture is proposed that enables strong approximation. We inform the discriminator of this GAN with the map between the prior input to the generator and the corresponding output samples, i.e. we introduce a `supervised GAN'. We compare the input-output map obtained with the standard GAN and supervised GAN and show experimentally that the standard GAN may fail to provide a path-wise approximation. The GAN is trained on a dataset obtained with exact simulation. The architecture was tested on geometric Brownian motion (GBM) and the Cox-Ingersoll-Ross (CIR) process. The supervised GAN outperformed the Euler and Milstein schemes in strong error on a discretisation with large time steps. It also outperformed the standard conditional GAN when approximating the conditional distribution. We also demonstrate how standard GANs may give rise to non-parsimonious input-output maps that are sensitive to perturbations, which motivates the need for constraints and regularisation on GAN generators.

The Seven-League Scheme: Deep learning for large time step Monte Carlo simulations of stochastic differential equations

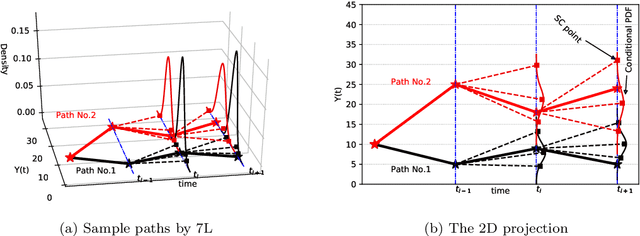
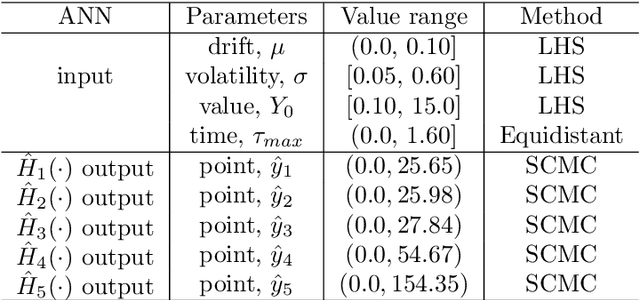
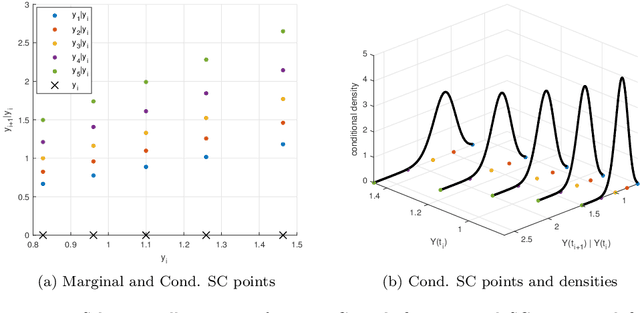
We propose an accurate data-driven numerical scheme to solve Stochastic Differential Equations (SDEs), by taking large time steps. The SDE discretization is built up by means of a polynomial chaos expansion method, on the basis of accurately determined stochastic collocation (SC) points. By employing an artificial neural network to learn these SC points, we can perform Monte Carlo simulations with large time steps. Error analysis confirms that this data-driven scheme results in accurate SDE solutions in the sense of strong convergence, provided the learning methodology is robust and accurate. With a variant method called the compression-decompression collocation and interpolation technique, we can drastically reduce the number of neural network functions that have to be learned, so that computational speed is enhanced. Numerical results show the high quality strong convergence error results, when using large time steps, and the novel scheme outperforms some classical numerical SDE discretizations. Some applications, here in financial option valuation, are also presented.

On Calibration Neural Networks for extracting implied information from American options

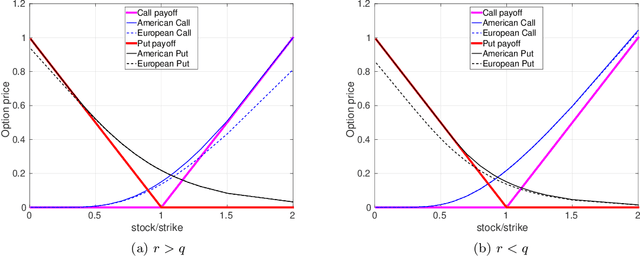
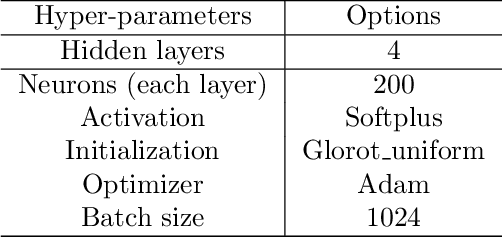
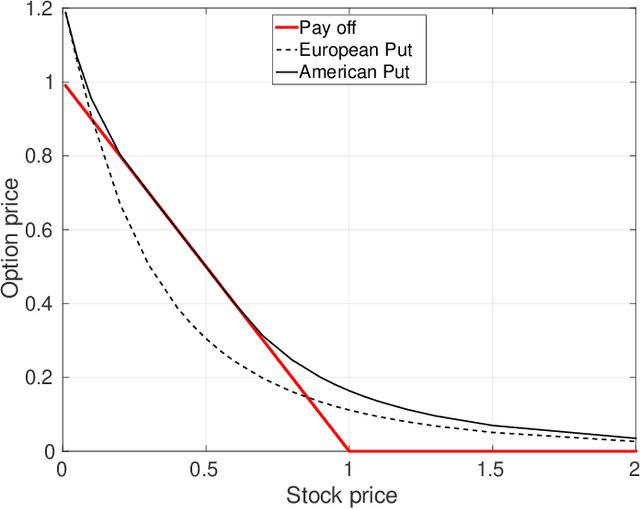
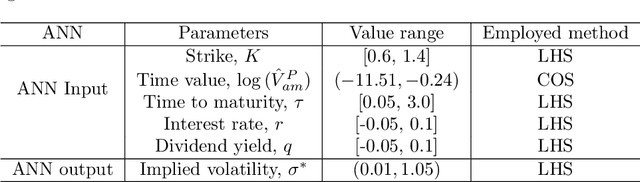
Extracting implied information, like volatility and/or dividend, from observed option prices is a challenging task when dealing with American options, because of the computational costs needed to solve the corresponding mathematical problem many thousands of times. We will employ a data-driven machine learning approach to estimate the Black-Scholes implied volatility and the dividend yield for American options in a fast and robust way. To determine the implied volatility, the inverse function is approximated by an artificial neural network on the computational domain of interest, which decouples the offline (training) and online (prediction) phases and thus eliminates the need for an iterative process. For the implied dividend yield, we formulate the inverse problem as a calibration problem and determine simultaneously the implied volatility and dividend yield. For this, a generic and robust calibration framework, the Calibration Neural Network (CaNN), is introduced to estimate multiple parameters. It is shown that machine learning can be used as an efficient numerical technique to extract implied information from American options.

A neural network-based framework for financial model calibration

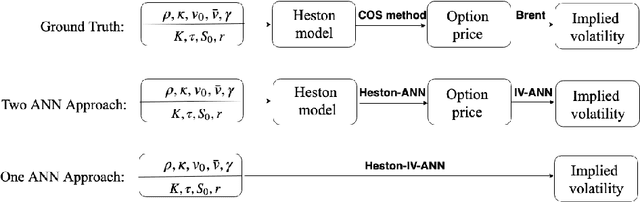
A data-driven approach called CaNN (Calibration Neural Network) is proposed to calibrate financial asset price models using an Artificial Neural Network (ANN). Determining optimal values of the model parameters is formulated as training hidden neurons within a machine learning framework, based on available financial option prices. The framework consists of two parts: a forward pass in which we train the weights of the ANN off-line, valuing options under many different asset model parameter settings; and a backward pass, in which we evaluate the trained ANN-solver on-line, aiming to find the weights of the neurons in the input layer. The rapid on-line learning of implied volatility by ANNs, in combination with the use of an adapted parallel global optimization method, tackles the computation bottleneck and provides a fast and reliable technique for calibrating model parameters while avoiding, as much as possible, getting stuck in local minima. Numerical experiments confirm that this machine-learning framework can be employed to calibrate parameters of high-dimensional stochastic volatility models efficiently and accurately.

Generalisation in fully-connected neural networks for time series forecasting

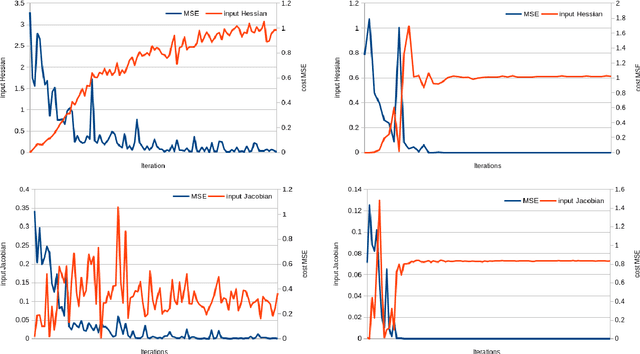
In this paper we study the generalisation capabilities of fully-connected neural networks trained in the context of time series forecasting. Time series do not satisfy the typical assumption in statistical learning theory of the data being i.i.d. samples from some data-generating distribution. We use the input and weight Hessians, that is the smoothness of the learned function with respect to the input and the width of the minimum in weight space, to quantify a network's ability to generalise to unseen data. While such generalisation metrics have been studied extensively in the i.i.d. setting of for example image recognition, here we empirically validate their use in the task of time series forecasting. Furthermore we discuss how one can control the generalisation capability of the network by means of the training process using the learning rate, batch size and the number of training iterations as controls. Using these hyperparameters one can efficiently control the complexity of the output function without imposing explicit constraints.

Pricing options and computing implied volatilities using neural networks

This paper proposes a data-driven approach, by means of an Artificial Neural Network (ANN), to value financial options and to calculate implied volatilities with the aim of accelerating the corresponding numerical methods. With ANNs being universal function approximators, this method trains an optimized ANN on a data set generated by a sophisticated financial model, and runs the trained ANN as an agent of the original solver in a fast and efficient way. We test this approach on three different types of solvers, including the analytic solution for the Black-Scholes equation, the COS method for the Heston stochastic volatility model and Brent's iterative root-finding method for the calculation of implied volatilities. The numerical results show that the ANN solver can reduce the computing time significantly.

Conditional Time Series Forecasting with Convolutional Neural Networks

We present a method for conditional time series forecasting based on an adaptation of the recent deep convolutional WaveNet architecture. The proposed network contains stacks of dilated convolutions that allow it to access a broad range of history when forecasting, a ReLU activation function and conditioning is performed by applying multiple convolutional filters in parallel to separate time series which allows for the fast processing of data and the exploitation of the correlation structure between the multivariate time series. We test and analyze the performance of the convolutional network both unconditionally as well as conditionally for financial time series forecasting using the S&P500, the volatility index, the CBOE interest rate and several exchange rates and extensively compare it to the performance of the well-known autoregressive model and a long-short term memory network. We show that a convolutional network is well-suited for regression-type problems and is able to effectively learn dependencies in and between the series without the need for long historical time series, is a time-efficient and easy to implement alternative to recurrent-type networks and tends to outperform linear and recurrent models.