Monte Carlo Simulation of SDEs using GANs

Generative adversarial networks (GANs) have shown promising results when applied on partial differential equations and financial time series generation. We investigate if GANs can also be used to approximate one-dimensional Ito stochastic differential equations (SDEs). We propose a scheme that approximates the path-wise conditional distribution of SDEs for large time steps. Standard GANs are only able to approximate processes in distribution, yielding a weak approximation to the SDE. A conditional GAN architecture is proposed that enables strong approximation. We inform the discriminator of this GAN with the map between the prior input to the generator and the corresponding output samples, i.e. we introduce a `supervised GAN'. We compare the input-output map obtained with the standard GAN and supervised GAN and show experimentally that the standard GAN may fail to provide a path-wise approximation. The GAN is trained on a dataset obtained with exact simulation. The architecture was tested on geometric Brownian motion (GBM) and the Cox-Ingersoll-Ross (CIR) process. The supervised GAN outperformed the Euler and Milstein schemes in strong error on a discretisation with large time steps. It also outperformed the standard conditional GAN when approximating the conditional distribution. We also demonstrate how standard GANs may give rise to non-parsimonious input-output maps that are sensitive to perturbations, which motivates the need for constraints and regularisation on GAN generators.

The Seven-League Scheme: Deep learning for large time step Monte Carlo simulations of stochastic differential equations

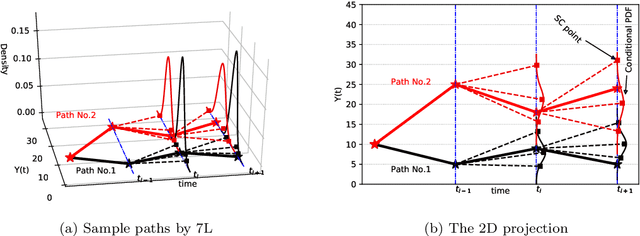
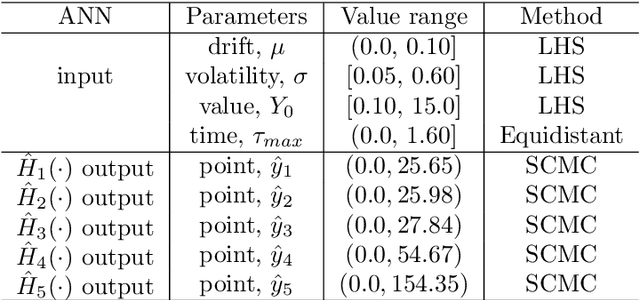
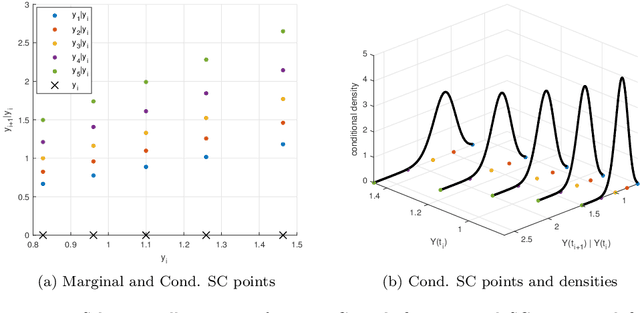
We propose an accurate data-driven numerical scheme to solve Stochastic Differential Equations (SDEs), by taking large time steps. The SDE discretization is built up by means of a polynomial chaos expansion method, on the basis of accurately determined stochastic collocation (SC) points. By employing an artificial neural network to learn these SC points, we can perform Monte Carlo simulations with large time steps. Error analysis confirms that this data-driven scheme results in accurate SDE solutions in the sense of strong convergence, provided the learning methodology is robust and accurate. With a variant method called the compression-decompression collocation and interpolation technique, we can drastically reduce the number of neural network functions that have to be learned, so that computational speed is enhanced. Numerical results show the high quality strong convergence error results, when using large time steps, and the novel scheme outperforms some classical numerical SDE discretizations. Some applications, here in financial option valuation, are also presented.

A neural network-based framework for financial model calibration

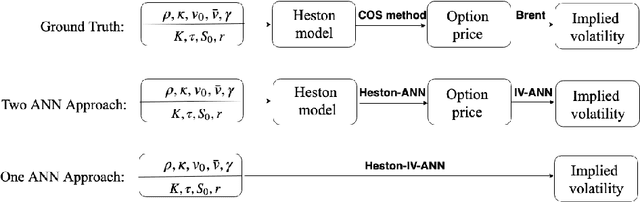
A data-driven approach called CaNN (Calibration Neural Network) is proposed to calibrate financial asset price models using an Artificial Neural Network (ANN). Determining optimal values of the model parameters is formulated as training hidden neurons within a machine learning framework, based on available financial option prices. The framework consists of two parts: a forward pass in which we train the weights of the ANN off-line, valuing options under many different asset model parameter settings; and a backward pass, in which we evaluate the trained ANN-solver on-line, aiming to find the weights of the neurons in the input layer. The rapid on-line learning of implied volatility by ANNs, in combination with the use of an adapted parallel global optimization method, tackles the computation bottleneck and provides a fast and reliable technique for calibrating model parameters while avoiding, as much as possible, getting stuck in local minima. Numerical experiments confirm that this machine-learning framework can be employed to calibrate parameters of high-dimensional stochastic volatility models efficiently and accurately.