Federated Learning and Unlearning for Recommendation with Personalized Data Sharing

Federated recommender systems (FedRS) have emerged as a paradigm for protecting user privacy by keeping interaction data on local devices while coordinating model training through a central server. However, most existing federated recommender systems adopt a one-size-fits-all assumption on user privacy, where all users are required to keep their data strictly local. This setting overlooks users who are willing to share their data with the server in exchange for better recommendation performance. Although several recent studies have explored personalized user data sharing in FedRS, they assume static user privacy preferences and cannot handle user requests to remove previously shared data and its corresponding influence on the trained model. To address this limitation, we propose FedShare, a federated learn-unlearn framework for recommender systems with personalized user data sharing. FedShare not only allows users to control how much interaction data is shared with the server, but also supports data unsharing requests by removing the influence of the unshared data from the trained model. Specifically, FedShare leverages shared data to construct a server-side high-order user-item graph and uses contrastive learning to jointly align local and global representations. In the unlearning phase, we design a contrastive unlearning mechanism that selectively removes representations induced by the unshared data using a small number of historical embedding snapshots, avoiding the need to store large amounts of historical gradient information as required by existing federated recommendation unlearning methods. Extensive experiments on three public datasets demonstrate that FedShare achieves strong recommendation performance in both the learning and unlearning phases, while significantly reducing storage overhead in the unlearning phase compared with state-of-the-art baselines.

Multi-stage feature decorrelation constraints for improving CNN classification performance

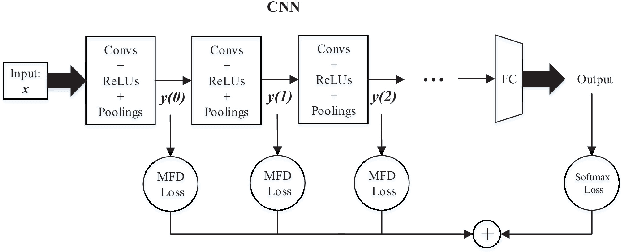
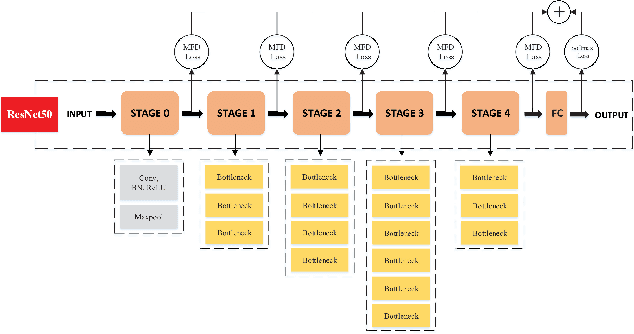
For the convolutional neural network (CNN) used for pattern classification, the training loss function is usually applied to the final output of the network, except for some regularization constraints on the network parameters. However, with the increasing of the number of network layers, the influence of the loss function on the network front layers gradually decreases, and the network parameters tend to fall into local optimization. At the same time, it is found that the trained network has significant information redundancy at all stages of features, which reduces the effectiveness of feature mapping at all stages and is not conducive to the change of the subsequent parameters of the network in the direction of optimality. Therefore, it is possible to obtain a more optimized solution of the network and further improve the classification accuracy of the network by designing a loss function for restraining the front stage features and eliminating the information redundancy of the front stage features .For CNN, this article proposes a multi-stage feature decorrelation loss (MFD Loss), which refines effective features and eliminates information redundancy by constraining the correlation of features at all stages. Considering that there are many layers in CNN, through experimental comparison and analysis, MFD Loss acts on multiple front layers of CNN, constrains the output features of each layer and each channel, and performs supervision training jointly with classification loss function during network training. Compared with the single Softmax Loss supervised learning, the experiments on several commonly used datasets on several typical CNNs prove that the classification performance of Softmax Loss+MFD Loss is significantly better. Meanwhile, the comparison experiments before and after the combination of MFD Loss and some other typical loss functions verify its good universality.

CHIEF: Clustering with Higher-order Motifs in Big Networks

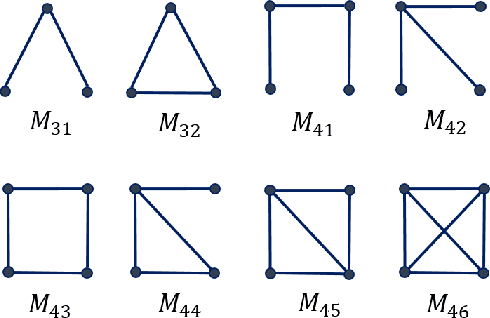
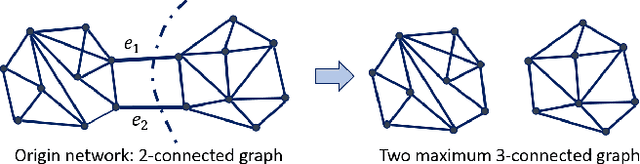
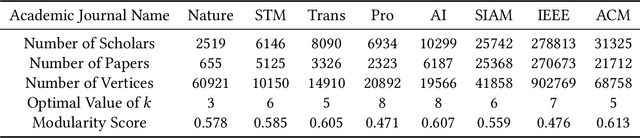
Clustering a group of vertices in networks facilitates applications across different domains, such as social computing and Internet of Things. However, challenges arises for clustering networks with increased scale. This paper proposes a solution which consists of two motif clustering techniques: standard acceleration CHIEF-ST and approximate acceleration CHIEF-AP. Both algorithms first find the maximal k-edge-connected subgraphs within the target networks to lower the network scale, then employ higher-order motifs in clustering. In the first procedure, we propose to lower the network scale by optimizing the network structure with maximal k-edge-connected subgraphs. For CHIEF-ST, we illustrate that all target motifs will be kept after this procedure when the minimum node degree of the target motif is equal or greater than k. For CHIEF-AP, we prove that the eigenvalues of the adjacency matrix and the Laplacian matrix are relatively stable after this step. That is, CHIEF-ST has no influence on motif clustering, whereas CHIEF-AP introduces limited yet acceptable impact. In the second procedure, we employ higher-order motifs, i.e., heterogeneous four-node motifs clustering in higher-order dense networks. The contributions of CHIEF are two-fold: (1) improved efficiency of motif clustering for big networks; (2) verification of higher-order motif significance. The proposed solutions are found to outperform baseline approaches according to experiments on real and synthetic networks, which demonstrates CHIEF's strength in large network analysis. Meanwhile, higher-order motifs are proved to perform better than traditional triangle motifs in clustering.

Searching Personalized $k$-wing in Large and Dynamic Bipartite Graphs

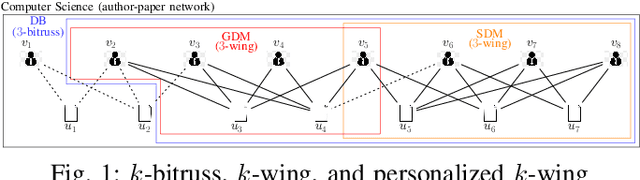
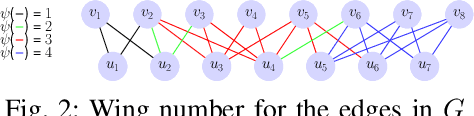
There are extensive studies focusing on the application scenario that all the bipartite cohesive subgraphs need to be discovered in a bipartite graph. However, we observe that, for some applications, one is interested in finding bipartite cohesive subgraphs containing a specific vertex. In this paper, we study a new query dependent bipartite cohesive subgraph search problem based on $k$-wing model, named as the personalized $k$-wing search problem. We introduce a $k$-wing equivalence relationship to summarize the edges of a bipartite graph $G$ into groups. Therefore, all the edges of $G$ are segregated into different groups, i.e. $k$-wing equivalence class, forming an efficient and wing number conserving index called EquiWing. Further, we propose a more compact version of EquiWing, EquiWing-Comp, which is achieved by integrating our proposed $k$-butterfly loose approach and discovered hierarchy properties. These indices are used to expedite the personalized $k$-wing search with a non-repetitive access to $G$, which leads to linear algorithms for searching the personalized $k$-wing. Moreover, we conduct a thorough study on the maintenance of the proposed indices for evolving bipartite graphs. We discover novel properties that help us localize the scope of the maintenance at a low cost. By exploiting the discoveries, we propose novel algorithms for maintaining the two indices, which substantially reduces the cost of maintenance. We perform extensive experimental studies in real, large-scale graphs to validate the efficiency and effectiveness of EquiWing and EquiWing-Comp compared to the baseline.