Aman Abidi
Searching Personalized $k$-wing in Large and Dynamic Bipartite Graphs
Jan 05, 2021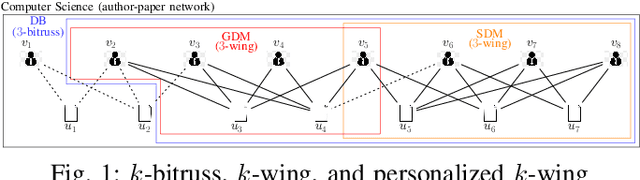

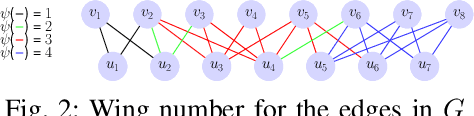

Abstract:There are extensive studies focusing on the application scenario that all the bipartite cohesive subgraphs need to be discovered in a bipartite graph. However, we observe that, for some applications, one is interested in finding bipartite cohesive subgraphs containing a specific vertex. In this paper, we study a new query dependent bipartite cohesive subgraph search problem based on $k$-wing model, named as the personalized $k$-wing search problem. We introduce a $k$-wing equivalence relationship to summarize the edges of a bipartite graph $G$ into groups. Therefore, all the edges of $G$ are segregated into different groups, i.e. $k$-wing equivalence class, forming an efficient and wing number conserving index called EquiWing. Further, we propose a more compact version of EquiWing, EquiWing-Comp, which is achieved by integrating our proposed $k$-butterfly loose approach and discovered hierarchy properties. These indices are used to expedite the personalized $k$-wing search with a non-repetitive access to $G$, which leads to linear algorithms for searching the personalized $k$-wing. Moreover, we conduct a thorough study on the maintenance of the proposed indices for evolving bipartite graphs. We discover novel properties that help us localize the scope of the maintenance at a low cost. By exploiting the discoveries, we propose novel algorithms for maintaining the two indices, which substantially reduces the cost of maintenance. We perform extensive experimental studies in real, large-scale graphs to validate the efficiency and effectiveness of EquiWing and EquiWing-Comp compared to the baseline.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge