CHIEF: Clustering with Higher-order Motifs in Big Networks
Paper and Code
Apr 06, 2022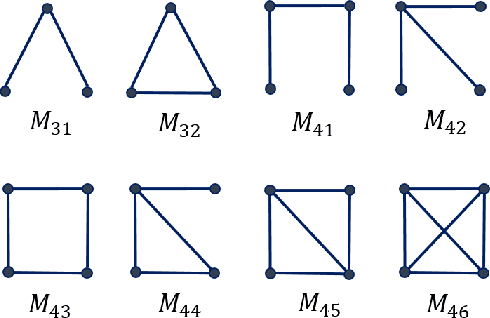

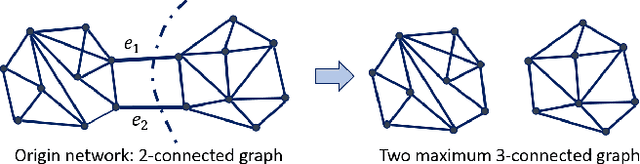
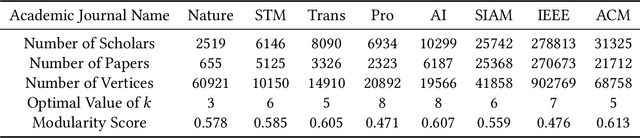
Clustering a group of vertices in networks facilitates applications across different domains, such as social computing and Internet of Things. However, challenges arises for clustering networks with increased scale. This paper proposes a solution which consists of two motif clustering techniques: standard acceleration CHIEF-ST and approximate acceleration CHIEF-AP. Both algorithms first find the maximal k-edge-connected subgraphs within the target networks to lower the network scale, then employ higher-order motifs in clustering. In the first procedure, we propose to lower the network scale by optimizing the network structure with maximal k-edge-connected subgraphs. For CHIEF-ST, we illustrate that all target motifs will be kept after this procedure when the minimum node degree of the target motif is equal or greater than k. For CHIEF-AP, we prove that the eigenvalues of the adjacency matrix and the Laplacian matrix are relatively stable after this step. That is, CHIEF-ST has no influence on motif clustering, whereas CHIEF-AP introduces limited yet acceptable impact. In the second procedure, we employ higher-order motifs, i.e., heterogeneous four-node motifs clustering in higher-order dense networks. The contributions of CHIEF are two-fold: (1) improved efficiency of motif clustering for big networks; (2) verification of higher-order motif significance. The proposed solutions are found to outperform baseline approaches according to experiments on real and synthetic networks, which demonstrates CHIEF's strength in large network analysis. Meanwhile, higher-order motifs are proved to perform better than traditional triangle motifs in clustering.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge