Coalitions of Large Language Models Increase the Robustness of AI Agents

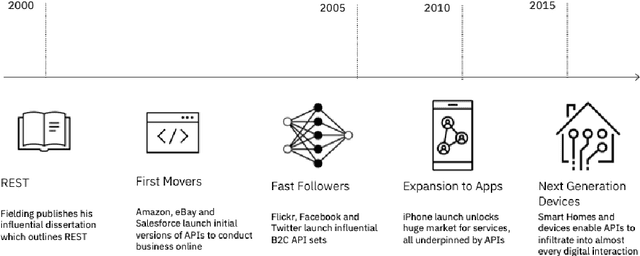
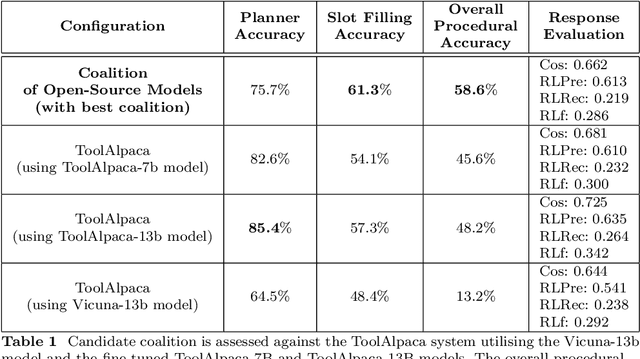
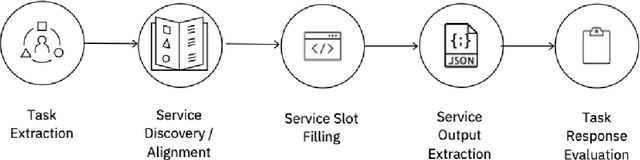
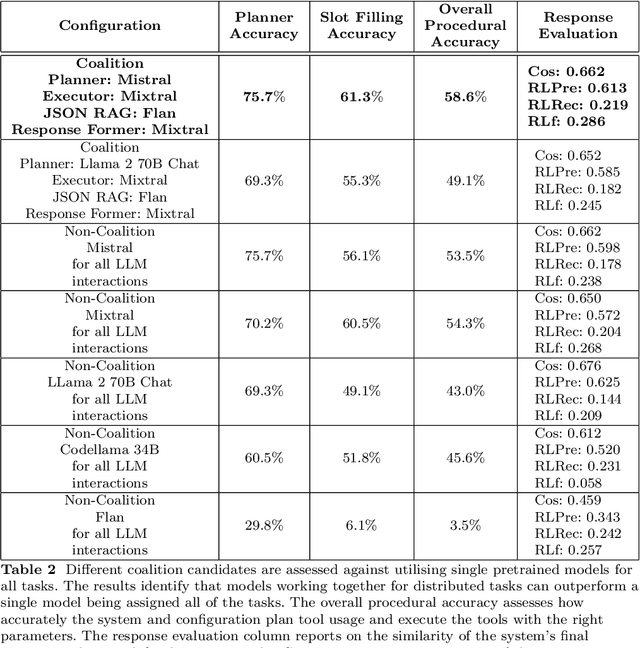
The emergence of Large Language Models (LLMs) have fundamentally altered the way we interact with digital systems and have led to the pursuit of LLM powered AI agents to assist in daily workflows. LLMs, whilst powerful and capable of demonstrating some emergent properties, are not logical reasoners and often struggle to perform well at all sub-tasks carried out by an AI agent to plan and execute a workflow. While existing studies tackle this lack of proficiency by generalised pretraining at a huge scale or by specialised fine-tuning for tool use, we assess if a system comprising of a coalition of pretrained LLMs, each exhibiting specialised performance at individual sub-tasks, can match the performance of single model agents. The coalition of models approach showcases its potential for building robustness and reducing the operational costs of these AI agents by leveraging traits exhibited by specific models. Our findings demonstrate that fine-tuning can be mitigated by considering a coalition of pretrained models and believe that this approach can be applied to other non-agentic systems which utilise LLMs.

Nonparametric Involutive Markov Chain Monte Carlo

A challenging problem in probabilistic programming is to develop inference algorithms that work for arbitrary programs in a universal probabilistic programming language (PPL). We present the nonparametric involutive Markov chain Monte Carlo (NP-iMCMC) algorithm as a method for constructing MCMC inference algorithms for nonparametric models expressible in universal PPLs. Building on the unifying involutive MCMC framework, and by providing a general procedure for driving state movement between dimensions, we show that NP-iMCMC can generalise numerous existing iMCMC algorithms to work on nonparametric models. We prove the correctness of the NP-iMCMC sampler. Our empirical study shows that the existing strengths of several iMCMC algorithms carry over to their nonparametric extensions. Applying our method to the recently proposed Nonparametric HMC, an instance of (Multiple Step) NP-iMCMC, we have constructed several nonparametric extensions (all of which new) that exhibit significant performance improvements.

Nonparametric Hamiltonian Monte Carlo

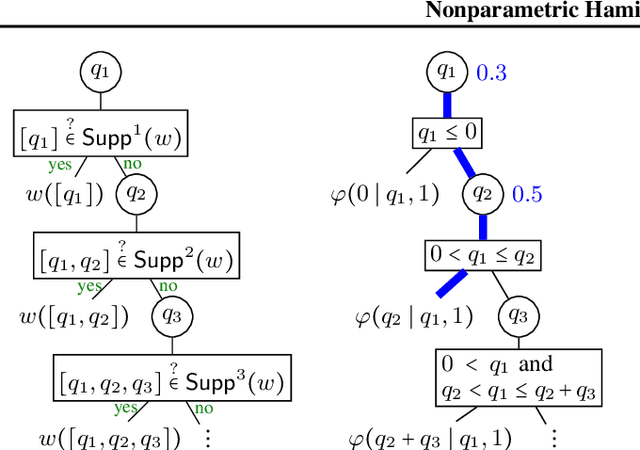
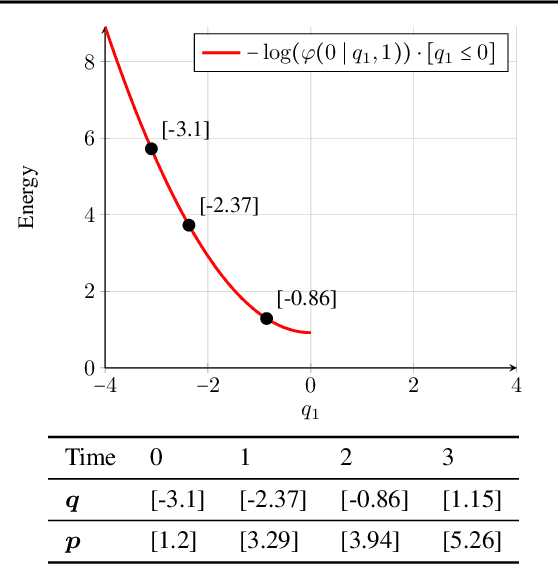
Probabilistic programming uses programs to express generative models whose posterior probability is then computed by built-in inference engines. A challenging goal is to develop general purpose inference algorithms that work out-of-the-box for arbitrary programs in a universal probabilistic programming language (PPL). The densities defined by such programs, which may use stochastic branching and recursion, are (in general) nonparametric, in the sense that they correspond to models on an infinite-dimensional parameter space. However standard inference algorithms, such as the Hamiltonian Monte Carlo (HMC) algorithm, target distributions with a fixed number of parameters. This paper introduces the Nonparametric Hamiltonian Monte Carlo (NP-HMC) algorithm which generalises HMC to nonparametric models. Inputs to NP-HMC are a new class of measurable functions called "tree representable", which serve as a language-independent representation of the density functions of probabilistic programs in a universal PPL. We provide a correctness proof of NP-HMC, and empirically demonstrate significant performance improvements over existing approaches on several nonparametric examples.

Densities of almost-surely terminating probabilistic programs are differentiable almost everywhere

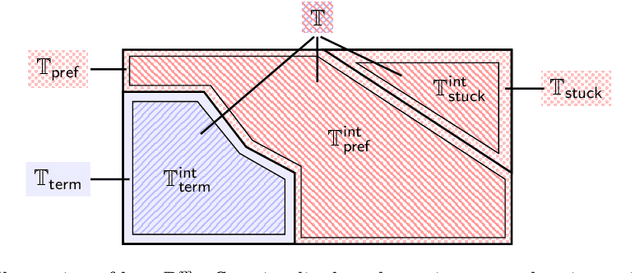
We study the differential properties of higher-order statistical probabilistic programs with recursion and conditioning. Our starting point is an open problem posed by Hongseok Yang: what class of statistical probabilistic programs have densities that are differentiable almost everywhere? To formalise the problem, we consider Statistical PCF (SPCF), an extension of call-by-value PCF with real numbers, and constructs for sampling and conditioning. We give SPCF a sampling-style operational semantics a la Borgstrom et al., and study the associated weight (commonly referred to as the density) function and value function on the set of possible execution traces. Our main result is that almost-surely terminating SPCF programs, generated from a set of primitive functions (e.g. the set of analytic functions) satisfying mild closure properties, have weight and value functions that are almost-everywhere differentiable. We use a stochastic form of symbolic execution to reason about almost-everywhere differentiability. A by-product of this work is that almost-surely terminating deterministic (S)PCF programs with real parameters denote functions that are almost-everywhere differentiable. Our result is of practical interest, as almost-everywhere differentiability of the density function is required to hold for the correctness of major gradient-based inference algorithms.

A Differential-form Pullback Programming Language for Higher-order Reverse-mode Automatic Differentiation

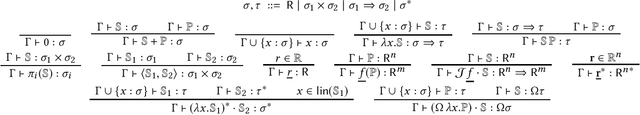
Building on the observation that reverse-mode automatic differentiation (AD) -- a generalisation of backpropagation -- can naturally be expressed as pullbacks of differential 1-forms, we design a simple higher-order programming language with a first-class differential operator, and present a reduction strategy which exactly simulates reverse-mode AD. We justify our reduction strategy by interpreting our language in any differential $\lambda$-category that satisfies the Hahn-Banach Separation Theorem, and show that the reduction strategy precisely captures reverse-mode AD in a truly higher-order setting.