Exact Bayesian Inference on Discrete Models via Probability Generating Functions: A Probabilistic Programming Approach

We present an exact Bayesian inference method for discrete statistical models, which can find exact solutions to many discrete inference problems, even with infinite support and continuous priors. To express such models, we introduce a probabilistic programming language that supports discrete and continuous sampling, discrete observations, affine functions, (stochastic) branching, and conditioning on events. Our key tool is probability generating functions: they provide a compact closed-form representation of distributions that are definable by programs, thus enabling the exact computation of posterior probabilities, expectation, variance, and higher moments. Our inference method is provably correct, fully automated and uses automatic differentiation (specifically, Taylor polynomials), but does not require computer algebra. Our experiments show that its performance on a range of real-world examples is competitive with approximate Monte Carlo methods, while avoiding approximation errors.

Nonparametric Involutive Markov Chain Monte Carlo

A challenging problem in probabilistic programming is to develop inference algorithms that work for arbitrary programs in a universal probabilistic programming language (PPL). We present the nonparametric involutive Markov chain Monte Carlo (NP-iMCMC) algorithm as a method for constructing MCMC inference algorithms for nonparametric models expressible in universal PPLs. Building on the unifying involutive MCMC framework, and by providing a general procedure for driving state movement between dimensions, we show that NP-iMCMC can generalise numerous existing iMCMC algorithms to work on nonparametric models. We prove the correctness of the NP-iMCMC sampler. Our empirical study shows that the existing strengths of several iMCMC algorithms carry over to their nonparametric extensions. Applying our method to the recently proposed Nonparametric HMC, an instance of (Multiple Step) NP-iMCMC, we have constructed several nonparametric extensions (all of which new) that exhibit significant performance improvements.

Guaranteed Bounds for Posterior Inference in Universal Probabilistic Programming

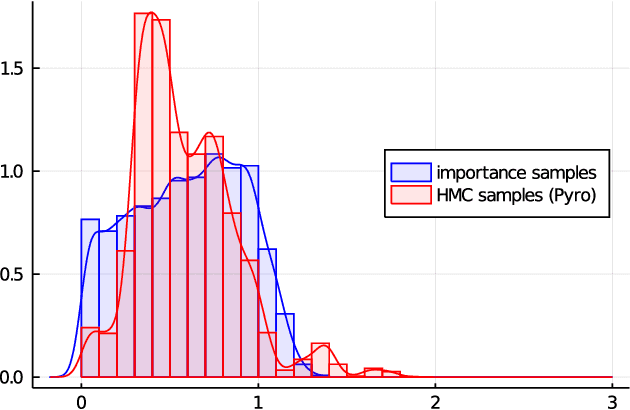
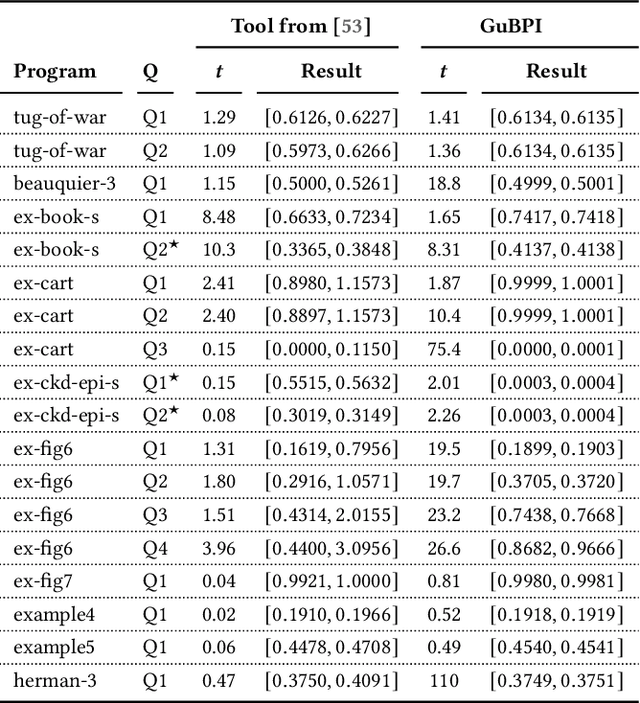
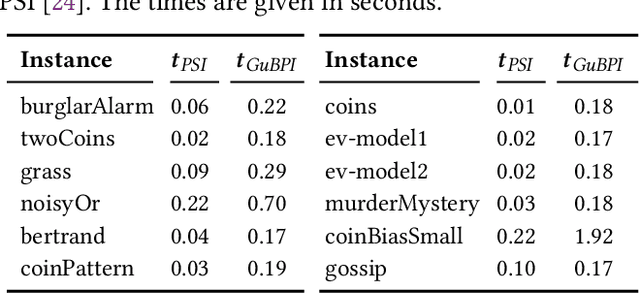
We propose a new method to approximate the posterior distribution of probabilistic programs by means of computing guaranteed bounds. The starting point of our work is an interval-based trace semantics for a recursive, higher-order probabilistic programming language with continuous distributions. Taking the form of (super-/subadditive) measures, these lower/upper bounds are non-stochastic and provably correct: using the semantics, we prove that the actual posterior of a given program is sandwiched between the lower and upper bounds (soundness); moreover the bounds converge to the posterior (completeness). As a practical and sound approximation, we introduce a weight-aware interval type system, which automatically infers interval bounds on not just the return value but also weight of program executions, simultaneously. We have built a tool implementation, called GuBPI, which automatically computes these posterior lower/upper bounds. Our evaluation on examples from the literature shows that the bounds are useful, and can even be used to recognise wrong outputs from stochastic posterior inference procedures.

Nonparametric Hamiltonian Monte Carlo

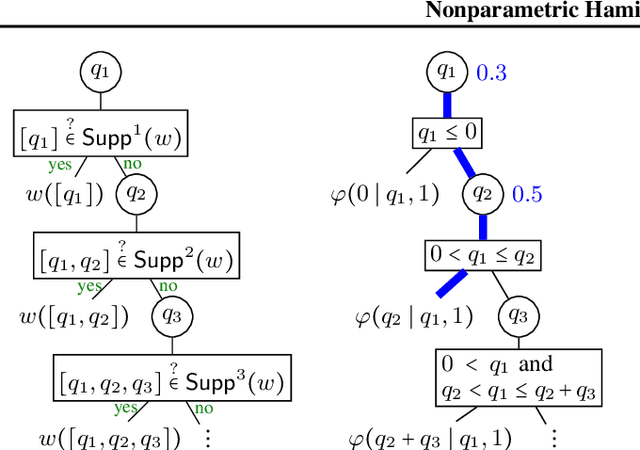
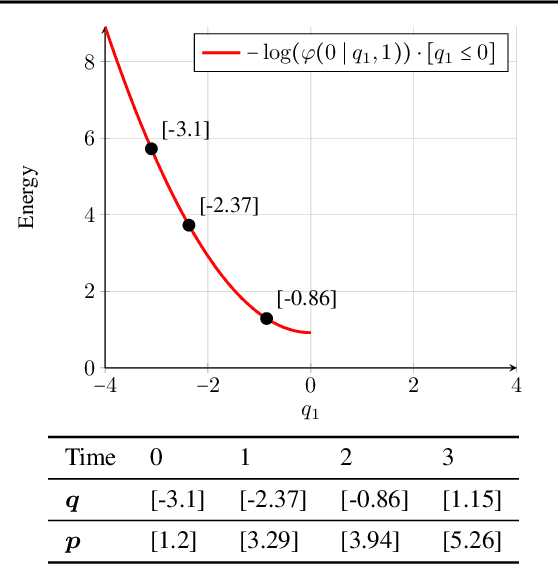
Probabilistic programming uses programs to express generative models whose posterior probability is then computed by built-in inference engines. A challenging goal is to develop general purpose inference algorithms that work out-of-the-box for arbitrary programs in a universal probabilistic programming language (PPL). The densities defined by such programs, which may use stochastic branching and recursion, are (in general) nonparametric, in the sense that they correspond to models on an infinite-dimensional parameter space. However standard inference algorithms, such as the Hamiltonian Monte Carlo (HMC) algorithm, target distributions with a fixed number of parameters. This paper introduces the Nonparametric Hamiltonian Monte Carlo (NP-HMC) algorithm which generalises HMC to nonparametric models. Inputs to NP-HMC are a new class of measurable functions called "tree representable", which serve as a language-independent representation of the density functions of probabilistic programs in a universal PPL. We provide a correctness proof of NP-HMC, and empirically demonstrate significant performance improvements over existing approaches on several nonparametric examples.