Non-Deterministic Planning for Hyperproperty Verification

Non-deterministic planning aims to find a policy that achieves a given objective in an environment where actions have uncertain effects, and the agent - potentially - only observes parts of the current state. Hyperproperties are properties that relate multiple paths of a system and can, e.g., capture security and information-flow policies. Popular logics for expressing temporal hyperproperties - such as HyperLTL - extend LTL by offering selective quantification over executions of a system. In this paper, we show that planning offers a powerful intermediate language for the automated verification of hyperproperties. Concretely, we present an algorithm that, given a HyperLTL verification problem, constructs a non-deterministic multi-agent planning instance (in the form of a QDec-POMDP) that, when admitting a plan, implies the satisfaction of the verification problem. We show that for large fragments of HyperLTL, the resulting planning instance corresponds to a classical, FOND, or POND planning problem. We implement our encoding in a prototype verification tool and report on encouraging experimental results.

Monitoring Second-Order Hyperproperties

Hyperproperties express the relationship between multiple executions of a system. This is needed in many AI-related fields, such as knowledge representation and planning, to capture system properties related to knowledge, information flow, and privacy. In this paper, we study the monitoring of complex hyperproperties at runtime. Previous work in this area has either focused on the simpler problem of monitoring trace properties (which are sets of traces, while hyperproperties are sets of sets of traces) or on monitoring first-order hyperproperties, which are expressible in temporal logics with first-order quantification over traces, such as HyperLTL. We present the first monitoring algorithm for the much more expressive class of second-order hyperproperties. Second-order hyperproperties include system properties like common knowledge, which cannot be expressed in first-order logics like HyperLTL. We introduce Hyper$^2$LTL$_f$, a temporal logic over finite traces that allows for second-order quantification over sets of traces. We study the monitoring problem in two fundamental execution models: (1) the parallel model, where a fixed number of traces is monitored in parallel, and (2) the sequential model, where an unbounded number of traces is observed sequentially, one trace after the other. For the parallel model, we show that the monitoring of the second-order hyperproperties of Hyper$^2$LTL$_f$ can be reduced to monitoring first-order hyperproperties. For the sequential model, we present a monitoring algorithm that handles second-order quantification efficiently, exploiting optimizations based on the monotonicity of subformulas, graph-based storing of executions, and fixpoint hashing. We present experimental results from a range of benchmarks, including examples from common knowledge and planning.

Hyper Strategy Logic

Strategy logic (SL) is a powerful temporal logic that enables strategic reasoning in multi-agent systems. SL supports explicit (first-order) quantification over strategies and provides a logical framework to express many important properties such as Nash equilibria, dominant strategies, etc. While in SL the same strategy can be used in multiple strategy profiles, each such profile is evaluated w.r.t. a path-property, i.e., a property that considers the single path resulting from a particular strategic interaction. In this paper, we present Hyper Strategy Logic (HyperSL), a strategy logic where the outcome of multiple strategy profiles can be compared w.r.t. a hyperproperty, i.e., a property that relates multiple paths. We show that HyperSL can capture important properties that cannot be expressed in SL, including non-interference, quantitative Nash equilibria, optimal adversarial planning, and reasoning under imperfect information. On the algorithmic side, we identify an expressive fragment of HyperSL with decidable model checking and present a model-checking algorithm. We contribute a prototype implementation of our algorithm and report on encouraging experimental results.

On Alternating-time Temporal Logic, Hyperproperties, and Strategy Sharing

Alternating-time temporal logic (ATL$^*$) is a well-established framework for formal reasoning about multi-agent systems. However, while ATL$^*$ can reason about the strategic ability of agents (e.g., some coalition $A$ can ensure that a goal is reached eventually), we cannot compare multiple strategic interactions, nor can we require multiple agents to follow the same strategy. For example, we cannot state that coalition $A$ can reach a goal sooner (or more often) than some other coalition $A'$. In this paper, we propose HyperATLS$^*_S$, an extension of ATL$^*$ in which we can (1) compare the outcome of multiple strategic interactions w.r.t. a hyperproperty, i.e., a property that refers to multiple paths at the same time, and (2) enforce that some agents share the same strategy. We show that HyperATL$^*_S$ is a rich specification language that captures important AI-related properties that were out of reach of existing logics. We prove that model checking of HyperATL$^*_S$ on concurrent game structures is decidable. We implement our model-checking algorithm in a tool we call HyMASMC and evaluate it on a range of benchmarks.

Guaranteed Bounds for Posterior Inference in Universal Probabilistic Programming

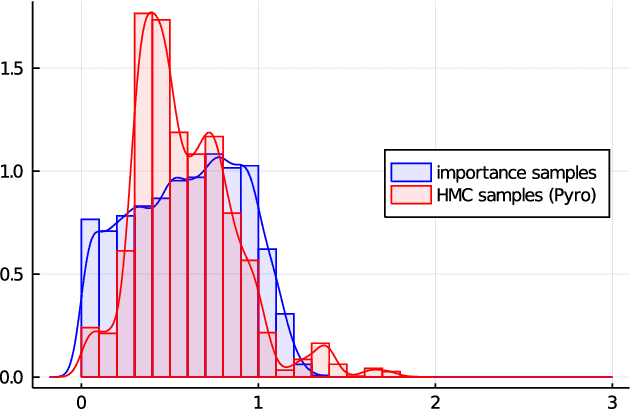
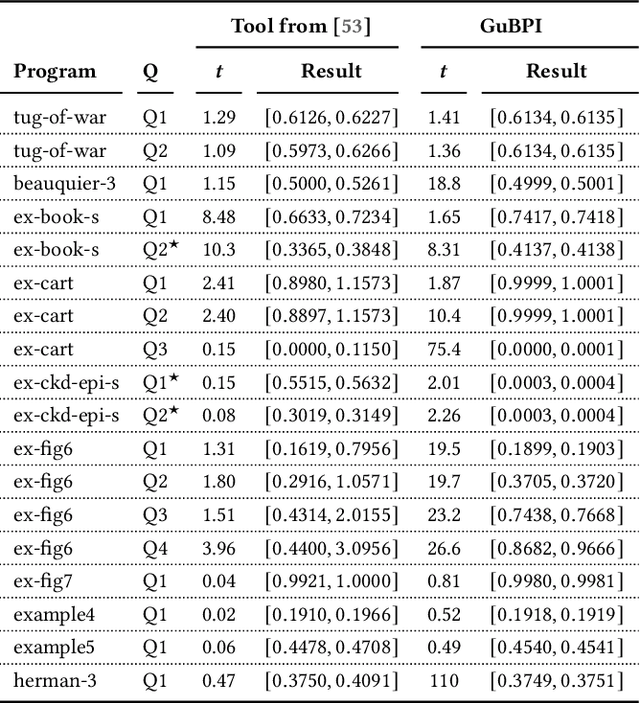
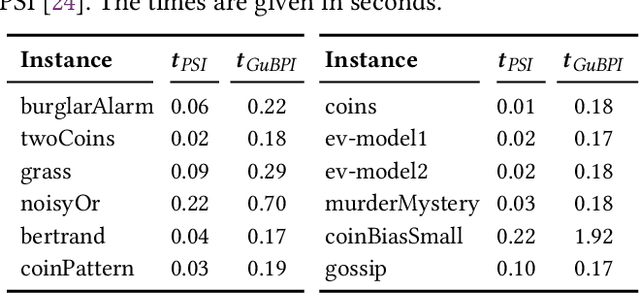
We propose a new method to approximate the posterior distribution of probabilistic programs by means of computing guaranteed bounds. The starting point of our work is an interval-based trace semantics for a recursive, higher-order probabilistic programming language with continuous distributions. Taking the form of (super-/subadditive) measures, these lower/upper bounds are non-stochastic and provably correct: using the semantics, we prove that the actual posterior of a given program is sandwiched between the lower and upper bounds (soundness); moreover the bounds converge to the posterior (completeness). As a practical and sound approximation, we introduce a weight-aware interval type system, which automatically infers interval bounds on not just the return value but also weight of program executions, simultaneously. We have built a tool implementation, called GuBPI, which automatically computes these posterior lower/upper bounds. Our evaluation on examples from the literature shows that the bounds are useful, and can even be used to recognise wrong outputs from stochastic posterior inference procedures.