Natural Synthesis: Outperforming Reactive Synthesis Tools with Large Reasoning Models

Reactive synthesis, the problem of automatically constructing a hardware circuit from a logical specification, is a long-standing challenge in formal verification. It is elusive for two reasons: It is algorithmically hard, and writing formal specifications by hand is notoriously difficult. In this paper, we tackle both sides of the problem. For the algorithmic side, we present a neuro-symbolic approach to reactive synthesis that couples large reasoning models with model checkers to iteratively repair a synthesized Verilog implementation via sound symbolic feedback. Our approach solves more benchmarks than the best dedicated tools in the annual synthesis competition and extends to constructing parameterized systems, a problem known to be undecidable. On the specification side, we introduce an autoformalization step that shifts the specification task from temporal logic to natural language by introducing a hand-authored dataset of natural-language specifications for evaluation. We demonstrate performance comparable to that of starting from formal specifications, establishing natural synthesis as a viable end-to-end workflow.

Monitoring Second-Order Hyperproperties

Hyperproperties express the relationship between multiple executions of a system. This is needed in many AI-related fields, such as knowledge representation and planning, to capture system properties related to knowledge, information flow, and privacy. In this paper, we study the monitoring of complex hyperproperties at runtime. Previous work in this area has either focused on the simpler problem of monitoring trace properties (which are sets of traces, while hyperproperties are sets of sets of traces) or on monitoring first-order hyperproperties, which are expressible in temporal logics with first-order quantification over traces, such as HyperLTL. We present the first monitoring algorithm for the much more expressive class of second-order hyperproperties. Second-order hyperproperties include system properties like common knowledge, which cannot be expressed in first-order logics like HyperLTL. We introduce Hyper$^2$LTL$_f$, a temporal logic over finite traces that allows for second-order quantification over sets of traces. We study the monitoring problem in two fundamental execution models: (1) the parallel model, where a fixed number of traces is monitored in parallel, and (2) the sequential model, where an unbounded number of traces is observed sequentially, one trace after the other. For the parallel model, we show that the monitoring of the second-order hyperproperties of Hyper$^2$LTL$_f$ can be reduced to monitoring first-order hyperproperties. For the sequential model, we present a monitoring algorithm that handles second-order quantification efficiently, exploiting optimizations based on the monotonicity of subformulas, graph-based storing of executions, and fixpoint hashing. We present experimental results from a range of benchmarks, including examples from common knowledge and planning.

Formal Specifications from Natural Language

We study the ability of language models to translate natural language into formal specifications with complex semantics. In particular, we fine-tune off-the-shelf language models on three datasets consisting of structured English sentences and their corresponding formal representation: 1) First-order logic (FOL), commonly used in software verification and theorem proving; 2) linear-time temporal logic (LTL), which forms the basis for industrial hardware specification languages; and 3) regular expressions (regex), frequently used in programming and search. Our experiments show that, in these diverse domains, the language models achieve competitive performance to the respective state-of-the-art with the benefits of being easy to access, cheap to fine-tune, and without a particular need for domain-specific reasoning. Additionally, we show that the language models have a unique selling point: they benefit from their generalization capabilities from pre-trained knowledge on natural language, e.g., to generalize to unseen variable names.

Attention Flows for General Transformers

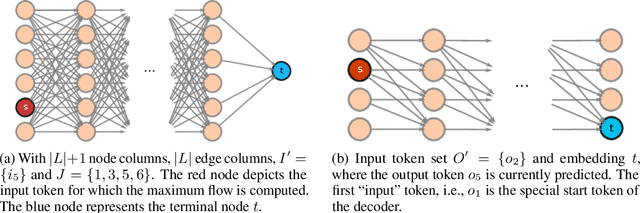
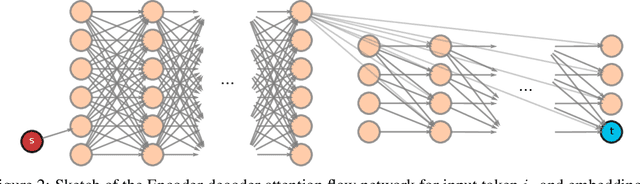
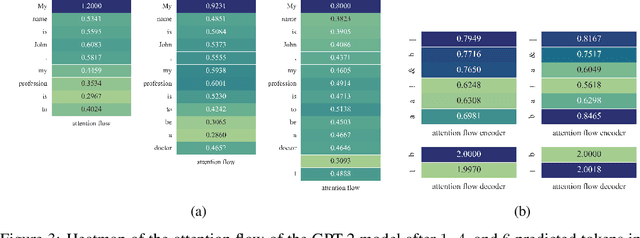
In this paper, we study the computation of how much an input token in a Transformer model influences its prediction. We formalize a method to construct a flow network out of the attention values of encoder-only Transformer models and extend it to general Transformer architectures including an auto-regressive decoder. We show that running a maxflow algorithm on the flow network construction yields Shapley values, which determine the impact of a player in cooperative game theory. By interpreting the input tokens in the flow network as players, we can compute their influence on the total attention flow leading to the decoder's decision. Additionally, we provide a library that computes and visualizes the attention flow of arbitrary Transformer models. We show the usefulness of our implementation on various models trained on natural language processing and reasoning tasks.