A Differential-form Pullback Programming Language for Higher-order Reverse-mode Automatic Differentiation
Paper and Code
Feb 19, 2020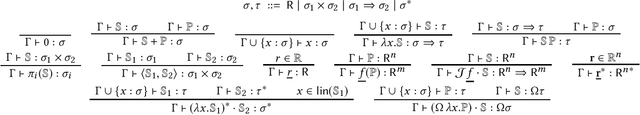


Building on the observation that reverse-mode automatic differentiation (AD) -- a generalisation of backpropagation -- can naturally be expressed as pullbacks of differential 1-forms, we design a simple higher-order programming language with a first-class differential operator, and present a reduction strategy which exactly simulates reverse-mode AD. We justify our reduction strategy by interpreting our language in any differential $\lambda$-category that satisfies the Hahn-Banach Separation Theorem, and show that the reduction strategy precisely captures reverse-mode AD in a truly higher-order setting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge