Coalitions of Large Language Models Increase the Robustness of AI Agents

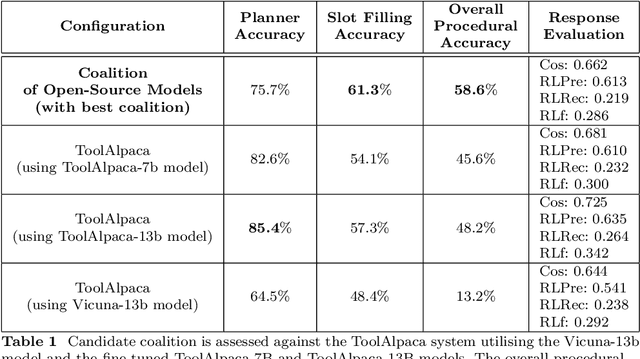
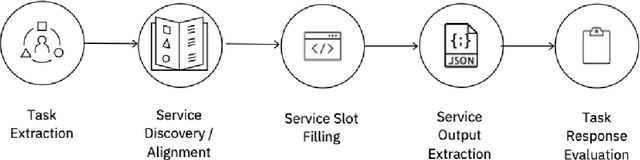
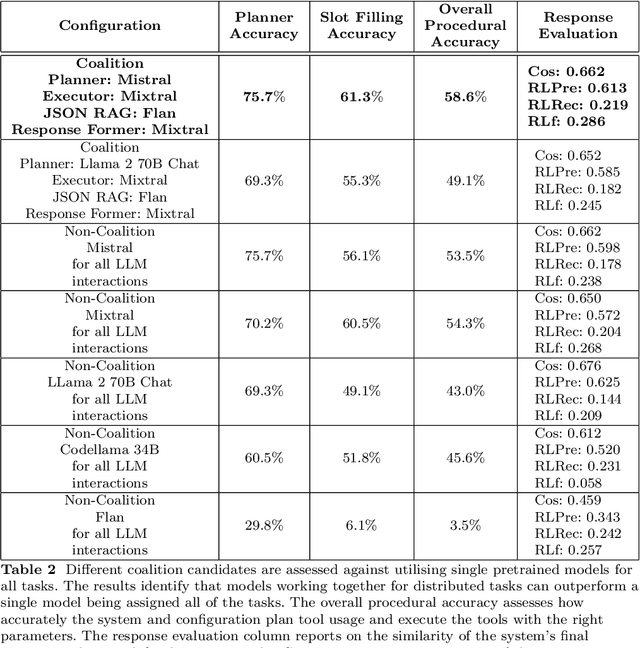
The emergence of Large Language Models (LLMs) have fundamentally altered the way we interact with digital systems and have led to the pursuit of LLM powered AI agents to assist in daily workflows. LLMs, whilst powerful and capable of demonstrating some emergent properties, are not logical reasoners and often struggle to perform well at all sub-tasks carried out by an AI agent to plan and execute a workflow. While existing studies tackle this lack of proficiency by generalised pretraining at a huge scale or by specialised fine-tuning for tool use, we assess if a system comprising of a coalition of pretrained LLMs, each exhibiting specialised performance at individual sub-tasks, can match the performance of single model agents. The coalition of models approach showcases its potential for building robustness and reducing the operational costs of these AI agents by leveraging traits exhibited by specific models. Our findings demonstrate that fine-tuning can be mitigated by considering a coalition of pretrained models and believe that this approach can be applied to other non-agentic systems which utilise LLMs.

Further Understanding of a Local Gaussian Process Approximation: Characterising Convergence in the Finite Regime

We show that common choices of kernel functions for a highly accurate and massively scalable nearest-neighbour based GP regression model (GPnn: \cite{GPnn}) exhibit gradual convergence to asymptotic behaviour as dataset-size $n$ increases. For isotropic kernels such as Mat\'{e}rn and squared-exponential, an upper bound on the predictive MSE can be obtained as $O(n^{-\frac{p}{d}})$ for input dimension $d$, $p$ dictated by the kernel (and $d>p$) and fixed number of nearest-neighbours $m$ with minimal assumptions on the input distribution. Similar bounds can be found under model misspecification and combined to give overall rates of convergence of both MSE and an important calibration metric. We show that lower bounds on $n$ can be given in terms of $m$, $l$, $p$, $d$, a tolerance $\varepsilon$ and a probability $\delta$. When $m$ is chosen to be $O(n^{\frac{p}{p+d}})$ minimax optimal rates of convergence are attained. Finally, we demonstrate empirical performance and show that in many cases convergence occurs faster than the upper bounds given here.

Leveraging Locality and Robustness to Achieve Massively Scalable Gaussian Process Regression

The accurate predictions and principled uncertainty measures provided by GP regression incur O(n^3) cost which is prohibitive for modern-day large-scale applications. This has motivated extensive work on computationally efficient approximations. We introduce a new perspective by exploring robustness properties and limiting behaviour of GP nearest-neighbour (GPnn) prediction. We demonstrate through theory and simulation that as the data-size n increases, accuracy of estimated parameters and GP model assumptions become increasingly irrelevant to GPnn predictive accuracy. Consequently, it is sufficient to spend small amounts of work on parameter estimation in order to achieve high MSE accuracy, even in the presence of gross misspecification. In contrast, as n tends to infinity, uncertainty calibration and NLL are shown to remain sensitive to just one parameter, the additive noise-variance; but we show that this source of inaccuracy can be corrected for, thereby achieving both well-calibrated uncertainty measures and accurate predictions at remarkably low computational cost. We exhibit a very simple GPnn regression algorithm with stand-out performance compared to other state-of-the-art GP approximations as measured on large UCI datasets. It operates at a small fraction of those other methods' training costs, for example on a basic laptop taking about 30 seconds to train on a dataset of size n = 1.6 x 10^6.

Provably Reliable Large-Scale Sampling from Gaussian Processes

When comparing approximate Gaussian process (GP) models, it can be helpful to be able to generate data from any GP. If we are interested in how approximate methods perform at scale, we may wish to generate very large synthetic datasets to evaluate them. Na\"{i}vely doing so would cost \(\mathcal{O}(n^3)\) flops and \(\mathcal{O}(n^2)\) memory to generate a size \(n\) sample. We demonstrate how to scale such data generation to large \(n\) whilst still providing guarantees that, with high probability, the sample is indistinguishable from a sample from the desired GP.