Carlos Alzate
Accelerated sparse Kernel Spectral Clustering for large scale data clustering problems
Oct 20, 2023



Abstract:An improved version of the sparse multiway kernel spectral clustering (KSC) is presented in this brief. The original algorithm is derived from weighted kernel principal component (KPCA) analysis formulated within the primal-dual least-squares support vector machine (LS-SVM) framework. Sparsity is achieved then by the combination of the incomplete Cholesky decomposition (ICD) based low rank approximation of the kernel matrix with the so called reduced set method. The original ICD based sparse KSC algorithm was reported to be computationally far too demanding, especially when applied on large scale data clustering problems that actually it was designed for, which has prevented to gain more than simply theoretical relevance so far. This is altered by the modifications reported in this brief that drastically improve the computational characteristics. Solving the alternative, symmetrized version of the computationally most demanding core eigenvalue problem eliminates the necessity of forming and SVD of large matrices during the model construction. This results in solving clustering problems now within seconds that were reported to require hours without altering the results. Furthermore, sparsity is also improved significantly, leading to more compact model representation, increasing further not only the computational efficiency but also the descriptive power. These transform the original, only theoretically relevant ICD based sparse KSC algorithm applicable for large scale practical clustering problems. Theoretical results and improvements are demonstrated by computational experiments on carefully selected synthetic data as well as on real life problems such as image segmentation.
Corpus Wide Argument Mining -- a Working Solution
Nov 25, 2019
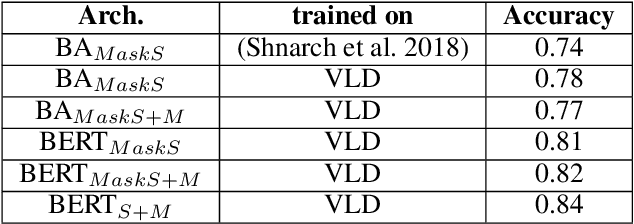


Abstract:One of the main tasks in argument mining is the retrieval of argumentative content pertaining to a given topic. Most previous work addressed this task by retrieving a relatively small number of relevant documents as the initial source for such content. This line of research yielded moderate success, which is of limited use in a real-world system. Furthermore, for such a system to yield a comprehensive set of relevant arguments, over a wide range of topics, it requires leveraging a large and diverse corpus in an appropriate manner. Here we present a first end-to-end high-precision, corpus-wide argument mining system. This is made possible by combining sentence-level queries over an appropriate indexing of a very large corpus of newspaper articles, with an iterative annotation scheme. This scheme addresses the inherent label bias in the data and pinpoints the regions of the sample space whose manual labeling is required to obtain high-precision among top-ranked candidates.
Kernel Spectral Clustering and applications
May 03, 2015



Abstract:In this chapter we review the main literature related to kernel spectral clustering (KSC), an approach to clustering cast within a kernel-based optimization setting. KSC represents a least-squares support vector machine based formulation of spectral clustering described by a weighted kernel PCA objective. Just as in the classifier case, the binary clustering model is expressed by a hyperplane in a high dimensional space induced by a kernel. In addition, the multi-way clustering can be obtained by combining a set of binary decision functions via an Error Correcting Output Codes (ECOC) encoding scheme. Because of its model-based nature, the KSC method encompasses three main steps: training, validation, testing. In the validation stage model selection is performed to obtain tuning parameters, like the number of clusters present in the data. This is a major advantage compared to classical spectral clustering where the determination of the clustering parameters is unclear and relies on heuristics. Once a KSC model is trained on a small subset of the entire data, it is able to generalize well to unseen test points. Beyond the basic formulation, sparse KSC algorithms based on the Incomplete Cholesky Decomposition (ICD) and $L_0$, $L_1, L_0 + L_1$, Group Lasso regularization are reviewed. In that respect, we show how it is possible to handle large scale data. Also, two possible ways to perform hierarchical clustering and a soft clustering method are presented. Finally, real-world applications such as image segmentation, power load time-series clustering, document clustering and big data learning are considered.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge