Raghvendra Mall
CASPER: Cross-modal Alignment of Spatial and single-cell Profiles for Expression Recovery
Nov 19, 2025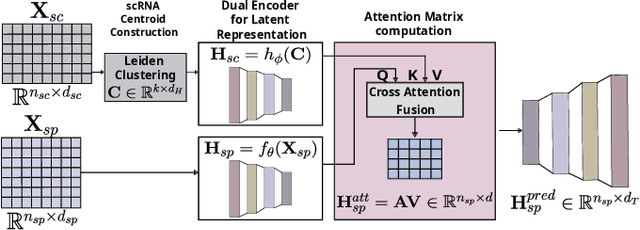
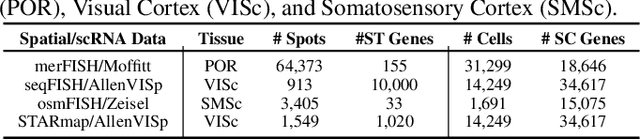
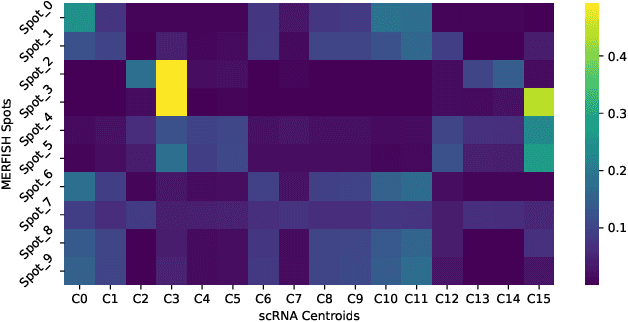
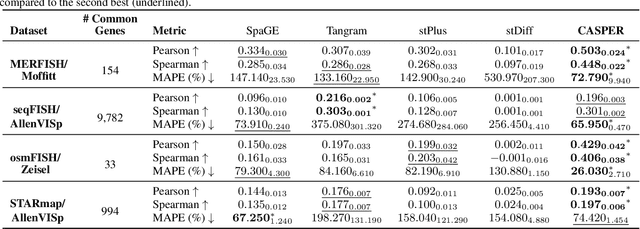
Abstract:Spatial Transcriptomics enables mapping of gene expression within its native tissue context, but current platforms measure only a limited set of genes due to experimental constraints and excessive costs. To overcome this, computational models integrate Single-Cell RNA Sequencing data with Spatial Transcriptomics to predict unmeasured genes. We propose CASPER, a cross-attention based framework that predicts unmeasured gene expression in Spatial Transcriptomics by leveraging centroid-level representations from Single-Cell RNA Sequencing. We performed rigorous testing over four state-of-the-art Spatial Transcriptomics/Single-Cell RNA Sequencing dataset pairs across four existing baseline models. CASPER shows significant improvement in nine out of the twelve metrics for our experiments. This work paves the way for further work in Spatial Transcriptomics to Single-Cell RNA Sequencing modality translation. The code for CASPER is available at https://github.com/AI4Med-Lab/CASPER.
Permutation-Invariant Subgraph Discovery
Apr 02, 2021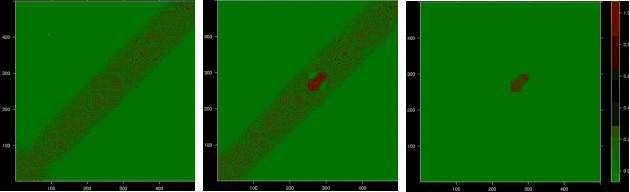
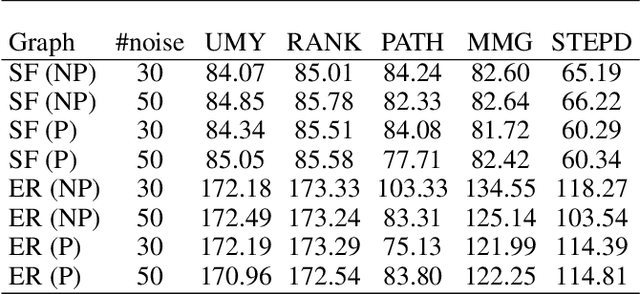

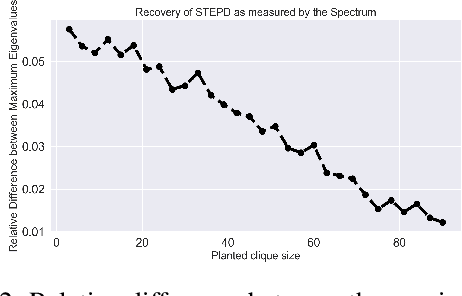
Abstract:We introduce Permutation and Structured Perturbation Inference (PSPI), a new problem formulation that abstracts many graph matching tasks that arise in systems biology. PSPI can be viewed as a robust formulation of the permutation inference or graph matching, where the objective is to find a permutation between two graphs under the assumption that a set of edges may have undergone a perturbation due to an underlying cause. For example, suppose there are two gene regulatory networks X and Y from a diseased and normal tissue respectively. Then, the PSPI problem can be used to detect if there has been a structural change between the two networks which can serve as a signature of the disease. Besides the new problem formulation, we propose an ADMM algorithm (STEPD) to solve a relaxed version of the PSPI problem. An extensive case study on comparative gene regulatory networks (GRNs) is used to demonstrate that STEPD is able to accurately infer structured perturbations and thus provides a tool for computational biologists to identify novel prognostic signatures. A spectral analysis confirms that STEPD can recover small clique-like perturbations making it a useful tool for detecting permutation-invariant changes in graphs.
Kernel Spectral Clustering and applications
May 03, 2015



Abstract:In this chapter we review the main literature related to kernel spectral clustering (KSC), an approach to clustering cast within a kernel-based optimization setting. KSC represents a least-squares support vector machine based formulation of spectral clustering described by a weighted kernel PCA objective. Just as in the classifier case, the binary clustering model is expressed by a hyperplane in a high dimensional space induced by a kernel. In addition, the multi-way clustering can be obtained by combining a set of binary decision functions via an Error Correcting Output Codes (ECOC) encoding scheme. Because of its model-based nature, the KSC method encompasses three main steps: training, validation, testing. In the validation stage model selection is performed to obtain tuning parameters, like the number of clusters present in the data. This is a major advantage compared to classical spectral clustering where the determination of the clustering parameters is unclear and relies on heuristics. Once a KSC model is trained on a small subset of the entire data, it is able to generalize well to unseen test points. Beyond the basic formulation, sparse KSC algorithms based on the Incomplete Cholesky Decomposition (ICD) and $L_0$, $L_1, L_0 + L_1$, Group Lasso regularization are reviewed. In that respect, we show how it is possible to handle large scale data. Also, two possible ways to perform hierarchical clustering and a soft clustering method are presented. Finally, real-world applications such as image segmentation, power load time-series clustering, document clustering and big data learning are considered.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge