Canlin Zhang
Minimum Description Length of a Spectrum Variational Autoencoder: A Theory
Apr 01, 2025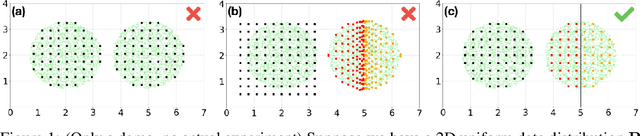
Abstract:Deep neural networks (DNNs) trained through end-to-end learning have achieved remarkable success across diverse machine learning tasks, yet they are not explicitly designed to adhere to the Minimum Description Length (MDL) principle, which posits that the best model provides the shortest description of the data. In this paper, we argue that MDL is essential to deep learning and propose a further generalized principle: Understanding is the use of a small amount of information to represent a large amount of information. To this end, we introduce a novel theoretical framework for designing and evaluating deep Variational Autoencoders (VAEs) based on MDL. In our theory, we designed the Spectrum VAE, a specific VAE architecture whose MDL can be rigorously evaluated under given conditions. Additionally, we introduce the concept of latent dimension combination, or pattern of spectrum, and provide the first theoretical analysis of their role in achieving MDL. We claim that a Spectrum VAE understands the data distribution in the most appropriate way when the MDL is achieved. This work is entirely theoretical and lays the foundation for future research on designing deep learning systems that explicitly adhere to information-theoretic principles.
Learning Regularities from Data using Spiking Functions: A Theory
May 19, 2024Abstract:Deep neural networks trained in an end-to-end manner are proven to be efficient in a wide range of machine learning tasks. However, there is one drawback of end-to-end learning: The learned features and information are implicitly represented in neural network parameters, which cannot be used as regularities, concepts or knowledge to explicitly represent the data probability distribution. To resolve this issue, we propose in this paper a new machine learning theory, which defines in mathematics what are regularities. Briefly, regularities are concise representations of the non-random features, or 'non-randomness' in the data probability distribution. Combining with information theory, we claim that regularities can also be regarded as a small amount of information encoding a large amount of information. Our theory is based on spiking functions. That is, if a function can react to, or spike on specific data samples more frequently than random noise inputs, we say that such a function discovers non-randomness from the data distribution, and encodes the non-randomness into regularities. Our theory also discusses applying multiple spiking functions to the same data distribution. In this process, we claim that the 'best' regularities, or the optimal spiking functions, are those who can capture the largest amount of information from the data distribution, and then encode the captured information in the most concise way. Theorems and hypotheses are provided to describe in mathematics what are 'best' regularities and optimal spiking functions. Finally, we propose a machine learning approach, which can potentially obtain the optimal spiking functions regarding the given dataset in practice.
Inductive Link Prediction in Knowledge Graphs using Path-based Neural Networks
Dec 16, 2023Abstract:Link prediction is a crucial research area in knowledge graphs, with many downstream applications. In many real-world scenarios, inductive link prediction is required, where predictions have to be made among unseen entities. Embedding-based models usually need fine-tuning on new entity embeddings, and hence are difficult to be directly applied to inductive link prediction tasks. Logical rules captured by rule-based models can be directly applied to new entities with the same graph typologies, but the captured rules are discrete and usually lack generosity. Graph neural networks (GNNs) can generalize topological information to new graphs taking advantage of deep neural networks, which however may still need fine-tuning on new entity embeddings. In this paper, we propose SiaILP, a path-based model for inductive link prediction using siamese neural networks. Our model only depends on relation and path embeddings, which can be generalized to new entities without fine-tuning. Experiments show that our model achieves several new state-of-the-art performances in link prediction tasks using inductive versions of WN18RR, FB15k-237, and Nell995.
Theoretical Knowledge Graph Reasoning via Ending Anchored Rules
Dec 15, 2020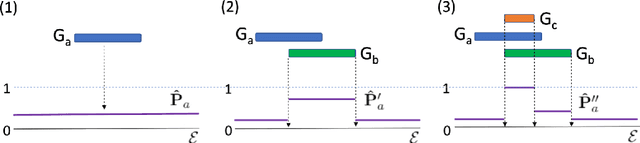

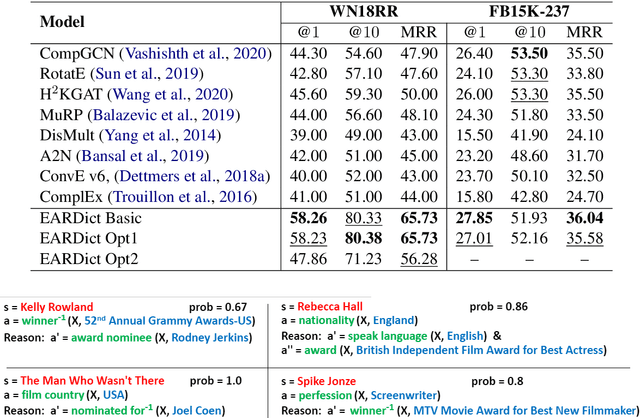
Abstract:Discovering precise and specific rules from knowledge graphs is regarded as an essential challenge, which can improve the performances of many downstream tasks and even provide new ways to approach some Natural Language Processing research topics. In this paper, we provide a fundamental theory for knowledge graph reasoning based on the ending anchored rules. Our theory provides precise reasons explaining why or why not a triple is correct. Then, we implement our theory by what we call the EARDict model. Results show that our EARDict model significantly outperforms all the benchmark models on two large datasets of knowledge graph completion, including achieving a Hits@10 score of 96.6 percent on WN18RR.
Preserving the Hypernym Tree of WordNet in Dense Embeddings
Apr 22, 2020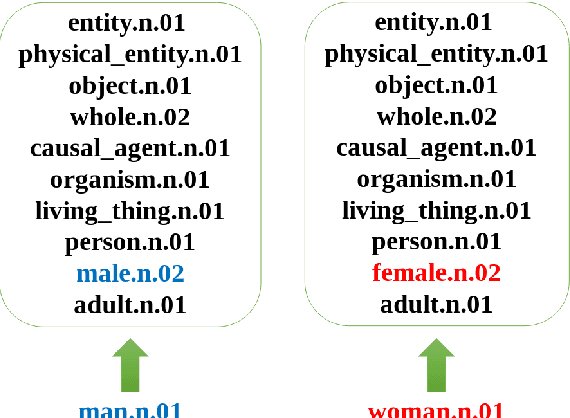
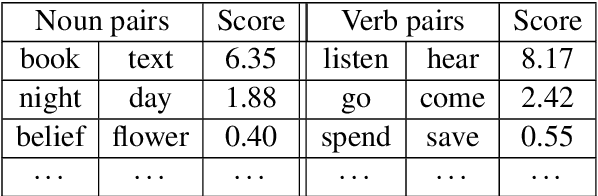
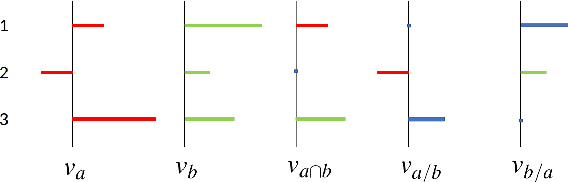
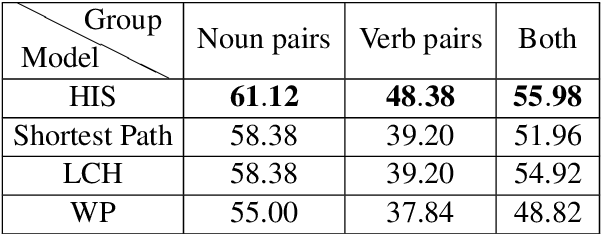
Abstract:In this paper, we provide a novel way to generate low-dimension (dense) vector embeddings for the noun and verb synsets in WordNet, so that the hypernym-hyponym tree structure is preserved in the embeddings. We call this embedding the sense spectrum (and sense spectra for embeddings). In order to create suitable labels for the training of sense spectra, we designed a new similarity measurement for noun and verb synsets in WordNet. We call this similarity measurement the hypernym intersection similarity (HIS), since it compares the common and unique hypernyms between two synsets. Our experiments show that on the noun and verb pairs of the SimLex-999 dataset, HIS outperforms the three similarity measurements in WordNet. Moreover, to the best of our knowledge, the sense spectra is the first dense embedding system that can explicitly and completely measure the hypernym-hyponym relationship in WordNet.
An Analysis on the Learning Rules of the Skip-Gram Model
Mar 18, 2020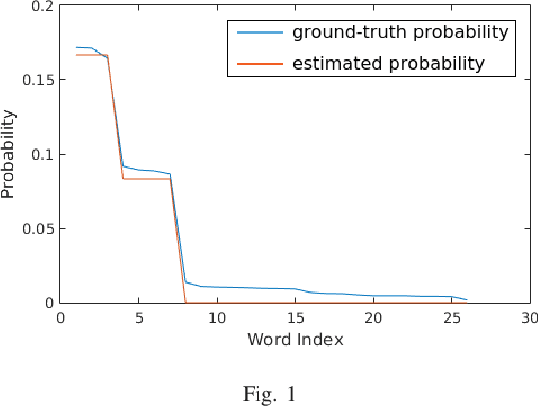
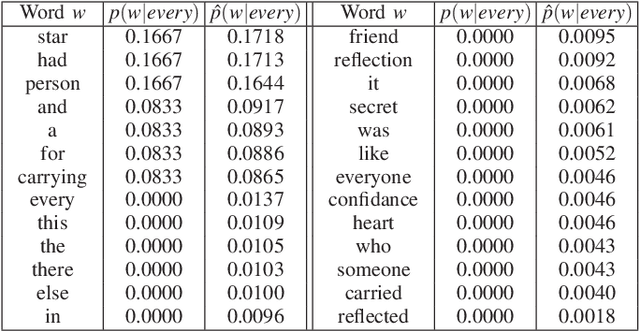
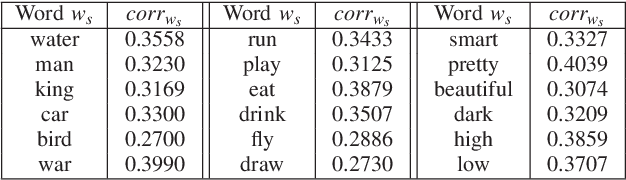
Abstract:To improve the generalization of the representations for natural language processing tasks, words are commonly represented using vectors, where distances among the vectors are related to the similarity of the words. While word2vec, the state-of-the-art implementation of the skip-gram model, is widely used and improves the performance of many natural language processing tasks, its mechanism is not yet well understood. In this work, we derive the learning rules for the skip-gram model and establish their close relationship to competitive learning. In addition, we provide the global optimal solution constraints for the skip-gram model and validate them by experimental results.
* Published on the 2019 International Joint Conference on Neural Networks
Towards Quantifying Intrinsic Generalization of Deep ReLU Networks
Oct 18, 2019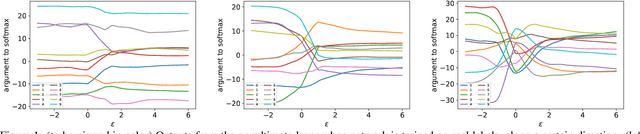
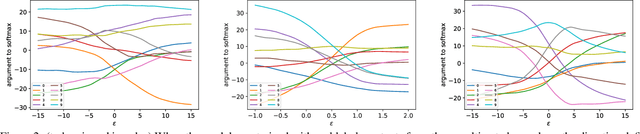
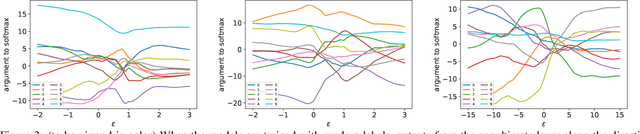
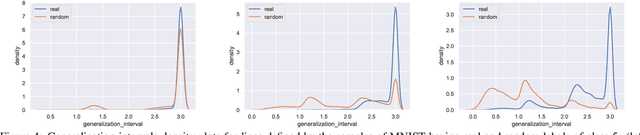
Abstract:Understanding the underlying mechanisms that enable the empirical successes of deep neural networks is essential for further improving their performance and explaining such networks. Towards this goal, a specific question is how to explain the "surprising" behavior of the same over-parametrized deep neural networks that can generalize well on real datasets and at the same time "memorize" training samples when the labels are randomized. In this paper, we demonstrate that deep ReLU networks generalize from training samples to new points via piece-wise linear interpolation. We provide a quantified analysis on the generalization ability of a deep ReLU network: Given a fixed point $\mathbf{x}$ and a fixed direction in the input space $\mathcal{S}$, there is always a segment such that any point on the segment will be classified the same as the fixed point $\mathbf{x}$. We call this segment the $generalization \ interval$. We show that the generalization intervals of a ReLU network behave similarly along pairwise directions between samples of the same label in both real and random cases on the MNIST and CIFAR-10 datasets. This result suggests that the same interpolation mechanism is used in both cases. Additionally, for datasets using real labels, such networks provide a good approximation of the underlying manifold in the data, where the changes are much smaller along tangent directions than along normal directions. On the other hand, however, for datasets with random labels, generalization intervals along mid-lines of triangles with the same label are much smaller than those on the datasets with real labels, suggesting different behaviors along other directions. Our systematic experiments demonstrate for the first time that such deep neural networks generalize through the same interpolation and explain the differences between their performance on datasets with real and random labels.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge