Towards Quantifying Intrinsic Generalization of Deep ReLU Networks

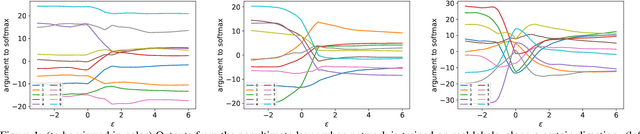
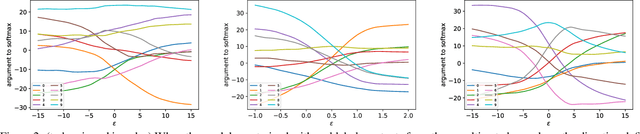
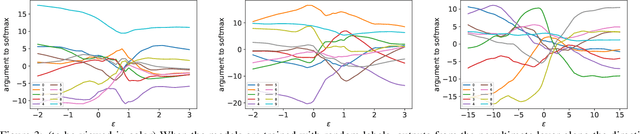
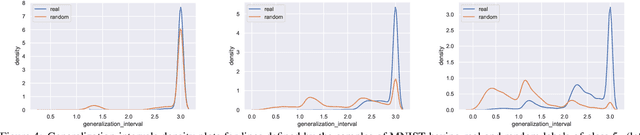
Understanding the underlying mechanisms that enable the empirical successes of deep neural networks is essential for further improving their performance and explaining such networks. Towards this goal, a specific question is how to explain the "surprising" behavior of the same over-parametrized deep neural networks that can generalize well on real datasets and at the same time "memorize" training samples when the labels are randomized. In this paper, we demonstrate that deep ReLU networks generalize from training samples to new points via piece-wise linear interpolation. We provide a quantified analysis on the generalization ability of a deep ReLU network: Given a fixed point $\mathbf{x}$ and a fixed direction in the input space $\mathcal{S}$, there is always a segment such that any point on the segment will be classified the same as the fixed point $\mathbf{x}$. We call this segment the $generalization \ interval$. We show that the generalization intervals of a ReLU network behave similarly along pairwise directions between samples of the same label in both real and random cases on the MNIST and CIFAR-10 datasets. This result suggests that the same interpolation mechanism is used in both cases. Additionally, for datasets using real labels, such networks provide a good approximation of the underlying manifold in the data, where the changes are much smaller along tangent directions than along normal directions. On the other hand, however, for datasets with random labels, generalization intervals along mid-lines of triangles with the same label are much smaller than those on the datasets with real labels, suggesting different behaviors along other directions. Our systematic experiments demonstrate for the first time that such deep neural networks generalize through the same interpolation and explain the differences between their performance on datasets with real and random labels.

Probing the Geometry of Data with Diffusion Fréchet Functions

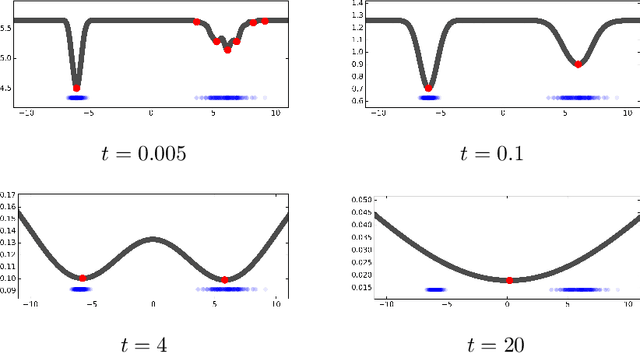
Many complex ecosystems, such as those formed by multiple microbial taxa, involve intricate interactions amongst various sub-communities. The most basic relationships are frequently modeled as co-occurrence networks in which the nodes represent the various players in the community and the weighted edges encode levels of interaction. In this setting, the composition of a community may be viewed as a probability distribution on the nodes of the network. This paper develops methods for modeling the organization of such data, as well as their Euclidean counterparts, across spatial scales. Using the notion of diffusion distance, we introduce diffusion Frechet functions and diffusion Frechet vectors associated with probability distributions on Euclidean space and the vertex set of a weighted network, respectively. We prove that these functional statistics are stable with respect to the Wasserstein distance between probability measures, thus yielding robust descriptors of their shapes. We apply the methodology to investigate bacterial communities in the human gut, seeking to characterize divergence from intestinal homeostasis in patients with Clostridium difficile infection (CDI) and the effects of fecal microbiota transplantation, a treatment used in CDI patients that has proven to be significantly more effective than traditional treatment with antibiotics. The proposed method proves useful in deriving a biomarker that might help elucidate the mechanisms that drive these processes.

The Shape of Data and Probability Measures

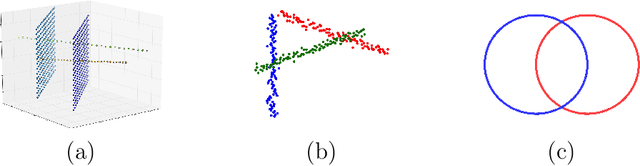
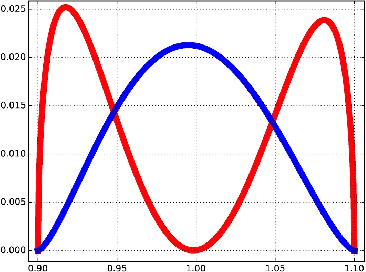
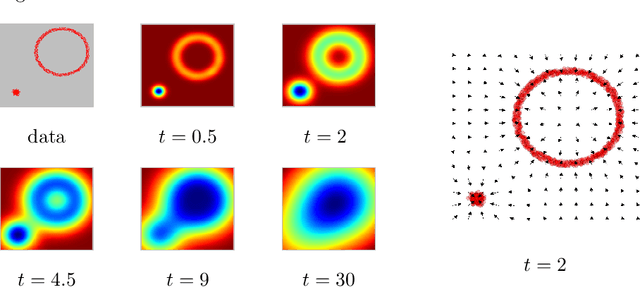
We introduce the notion of multiscale covariance tensor fields (CTF) associated with Euclidean random variables as a gateway to the shape of their distributions. Multiscale CTFs quantify variation of the data about every point in the data landscape at all spatial scales, unlike the usual covariance tensor that only quantifies global variation about the mean. Empirical forms of localized covariance previously have been used in data analysis and visualization, but we develop a framework for the systematic treatment of theoretical questions and computational models based on localized covariance. We prove strong stability theorems with respect to the Wasserstein distance between probability measures, obtain consistency results, as well as estimates for the rate of convergence of empirical CTFs. These results ensure that CTFs are robust to sampling, noise and outliers. We provide numerous illustrations of how CTFs let us extract shape from data and also apply CTFs to manifold clustering, the problem of categorizing data points according to their noisy membership in a collection of possibly intersecting, smooth submanifolds of Euclidean space. We prove that the proposed manifold clustering method is stable and carry out several experiments to validate the method.

The Phylogenetic LASSO and the Microbiome

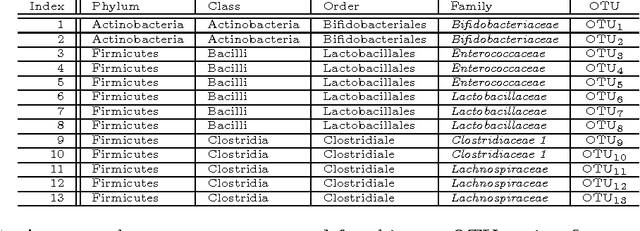
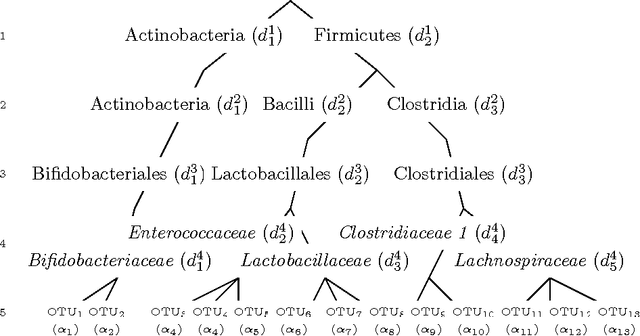
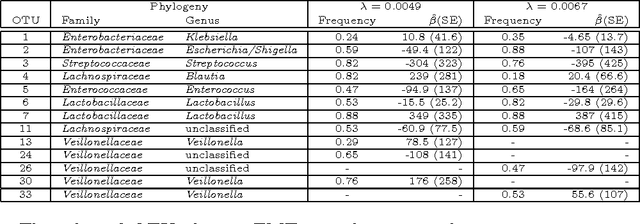
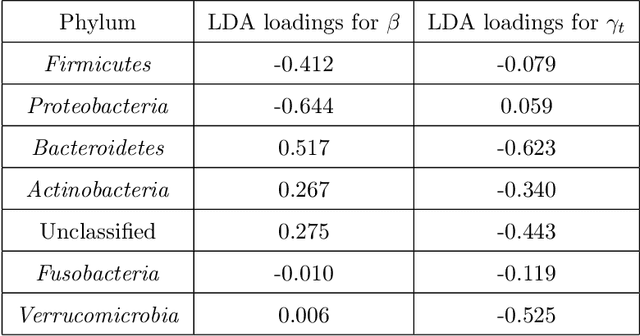
Scientific investigations that incorporate next generation sequencing involve analyses of high-dimensional data where the need to organize, collate and interpret the outcomes are pressingly important. Currently, data can be collected at the microbiome level leading to the possibility of personalized medicine whereby treatments can be tailored at this scale. In this paper, we lay down a statistical framework for this type of analysis with a view toward synthesis of products tailored to individual patients. Although the paper applies the technique to data for a particular infectious disease, the methodology is sufficiently rich to be expanded to other problems in medicine, especially those in which coincident `-omics' covariates and clinical responses are simultaneously captured.