The Shape of Data and Probability Measures
Paper and Code
Feb 28, 2017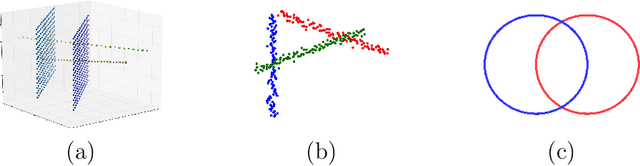


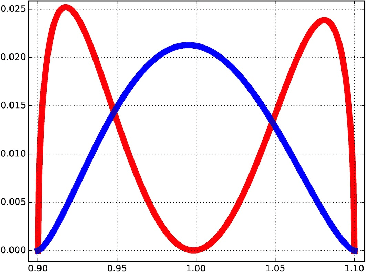
We introduce the notion of multiscale covariance tensor fields (CTF) associated with Euclidean random variables as a gateway to the shape of their distributions. Multiscale CTFs quantify variation of the data about every point in the data landscape at all spatial scales, unlike the usual covariance tensor that only quantifies global variation about the mean. Empirical forms of localized covariance previously have been used in data analysis and visualization, but we develop a framework for the systematic treatment of theoretical questions and computational models based on localized covariance. We prove strong stability theorems with respect to the Wasserstein distance between probability measures, obtain consistency results, as well as estimates for the rate of convergence of empirical CTFs. These results ensure that CTFs are robust to sampling, noise and outliers. We provide numerous illustrations of how CTFs let us extract shape from data and also apply CTFs to manifold clustering, the problem of categorizing data points according to their noisy membership in a collection of possibly intersecting, smooth submanifolds of Euclidean space. We prove that the proposed manifold clustering method is stable and carry out several experiments to validate the method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge