Bootstrapping the Cross-Validation Estimate

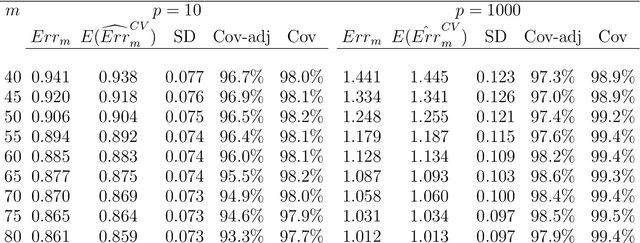
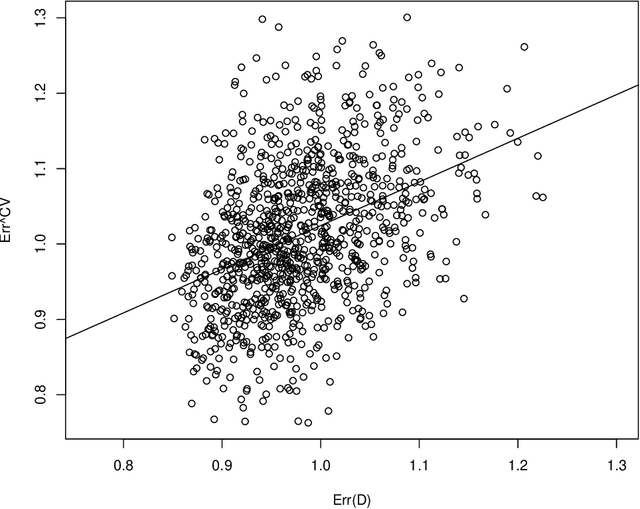
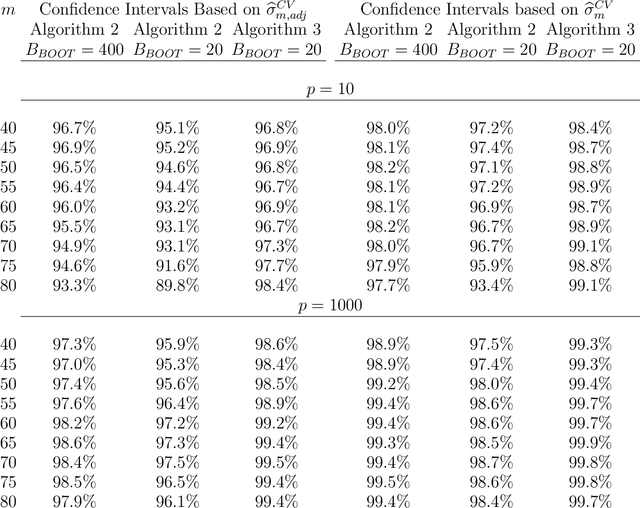
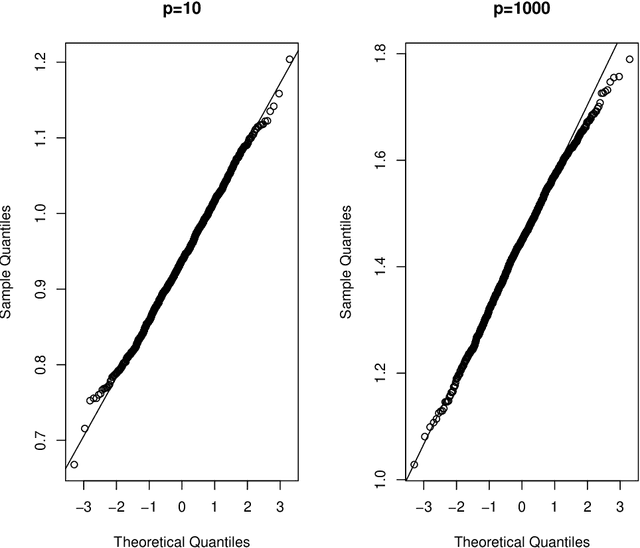
Cross-validation is a widely used technique for evaluating the performance of prediction models. It helps avoid the optimism bias in error estimates, which can be significant for models built using complex statistical learning algorithms. However, since the cross-validation estimate is a random value dependent on observed data, it is essential to accurately quantify the uncertainty associated with the estimate. This is especially important when comparing the performance of two models using cross-validation, as one must determine whether differences in error estimates are a result of chance fluctuations. Although various methods have been developed for making inferences on cross-validation estimates, they often have many limitations, such as stringent model assumptions This paper proposes a fast bootstrap method that quickly estimates the standard error of the cross-validation estimate and produces valid confidence intervals for a population parameter measuring average model performance. Our method overcomes the computational challenge inherent in bootstrapping the cross-validation estimate by estimating the variance component within a random effects model. It is just as flexible as the cross-validation procedure itself. To showcase the effectiveness of our approach, we employ comprehensive simulations and real data analysis across three diverse applications.

Hierarchical Pretraining for Biomedical Term Embeddings

Electronic health records (EHR) contain narrative notes that provide extensive details on the medical condition and management of patients. Natural language processing (NLP) of clinical notes can use observed frequencies of clinical terms as predictive features for downstream applications such as clinical decision making and patient trajectory prediction. However, due to the vast number of highly similar and related clinical concepts, a more effective modeling strategy is to represent clinical terms as semantic embeddings via representation learning and use the low dimensional embeddings as feature vectors for predictive modeling. To achieve efficient representation, fine-tuning pretrained language models with biomedical knowledge graphs may generate better embeddings for biomedical terms than those from standard language models alone. These embeddings can effectively discriminate synonymous pairs of from those that are unrelated. However, they often fail to capture different degrees of similarity or relatedness for concepts that are hierarchical in nature. To overcome this limitation, we propose HiPrBERT, a novel biomedical term representation model trained on additionally complied data that contains hierarchical structures for various biomedical terms. We modify an existing contrastive loss function to extract information from these hierarchies. Our numerical experiments demonstrate that HiPrBERT effectively learns the pair-wise distance from hierarchical information, resulting in a substantially more informative embeddings for further biomedical applications

Priv'IT: Private and Sample Efficient Identity Testing

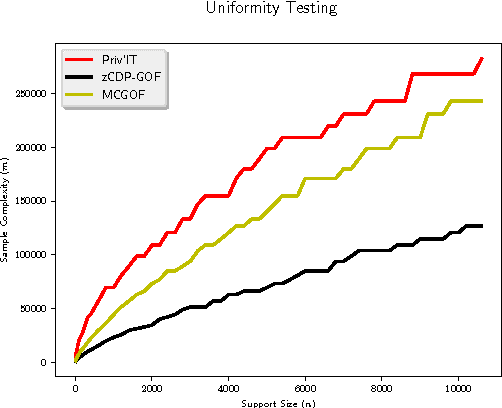
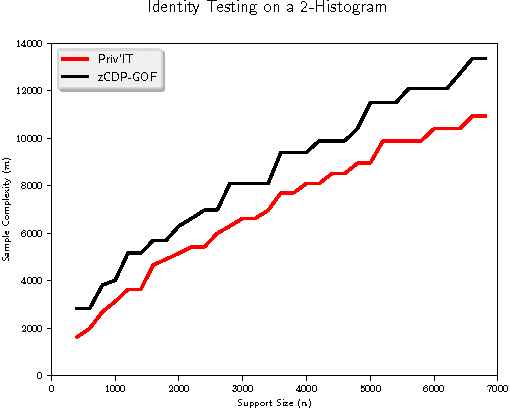
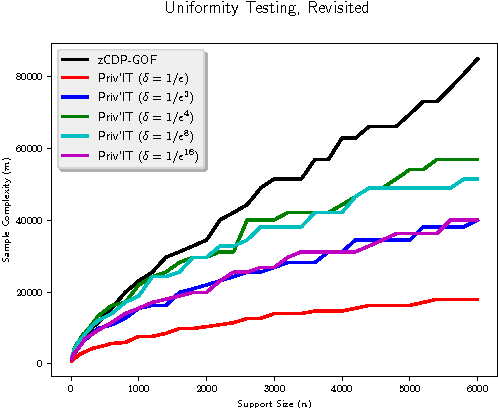
We develop differentially private hypothesis testing methods for the small sample regime. Given a sample $\cal D$ from a categorical distribution $p$ over some domain $\Sigma$, an explicitly described distribution $q$ over $\Sigma$, some privacy parameter $\varepsilon$, accuracy parameter $\alpha$, and requirements $\beta_{\rm I}$ and $\beta_{\rm II}$ for the type I and type II errors of our test, the goal is to distinguish between $p=q$ and $d_{\rm{TV}}(p,q) \geq \alpha$. We provide theoretical bounds for the sample size $|{\cal D}|$ so that our method both satisfies $(\varepsilon,0)$-differential privacy, and guarantees $\beta_{\rm I}$ and $\beta_{\rm II}$ type I and type II errors. We show that differential privacy may come for free in some regimes of parameters, and we always beat the sample complexity resulting from running the $\chi^2$-test with noisy counts, or standard approaches such as repetition for endowing non-private $\chi^2$-style statistics with differential privacy guarantees. We experimentally compare the sample complexity of our method to that of recently proposed methods for private hypothesis testing.