Infinite-Horizon Offline Reinforcement Learning with Linear Function Approximation: Curse of Dimensionality and Algorithm

In this paper, we investigate the sample complexity of policy evaluation in infinite-horizon offline reinforcement learning (also known as the off-policy evaluation problem) with linear function approximation. We identify a hard regime $d\gamma^{2}>1$, where $d$ is the dimension of the feature vector and $\gamma$ is the discount rate. In this regime, for any $q\in[\gamma^{2},1]$, we can construct a hard instance such that the smallest eigenvalue of its feature covariance matrix is $q/d$ and it requires $\Omega\left(\frac{d}{\gamma^{2}\left(q-\gamma^{2}\right)\varepsilon^{2}}\exp\left(\Theta\left(d\gamma^{2}\right)\right)\right)$ samples to approximate the value function up to an additive error $\varepsilon$. Note that the lower bound of the sample complexity is exponential in $d$. If $q=\gamma^{2}$, even infinite data cannot suffice. Under the low distribution shift assumption, we show that there is an algorithm that needs at most $O\left(\max\left\{ \frac{\left\Vert \theta^{\pi}\right\Vert _{2}^{4}}{\varepsilon^{4}}\log\frac{d}{\delta},\frac{1}{\varepsilon^{2}}\left(d+\log\frac{1}{\delta}\right)\right\} \right)$ samples ($\theta^{\pi}$ is the parameter of the policy in linear function approximation) and guarantees approximation to the value function up to an additive error of $\varepsilon$ with probability at least $1-\delta$.

Leverage the Average: an Analysis of Regularization in RL

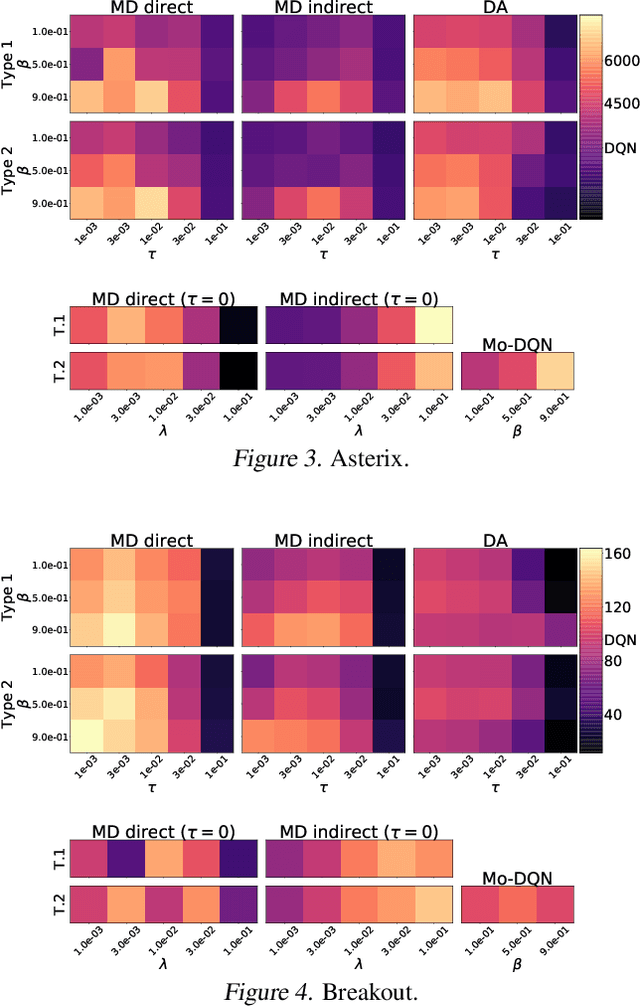
Building upon the formalism of regularized Markov decision processes, we study the effect of Kullback-Leibler (KL) and entropy regularization in reinforcement learning. Through an equivalent formulation of the related approximate dynamic programming (ADP) scheme, we show that a KL penalty amounts to averaging q-values. This equivalence allows drawing connections between a priori disconnected methods from the literature, and proving that a KL regularization indeed leads to averaging errors made at each iteration of value function update. With the proposed theoretical analysis, we also study the interplay between KL and entropy regularization. When the considered ADP scheme is combined with neural-network-based stochastic approximations, the equivalence is lost, which suggests a number of different ways to do regularization. Because this goes beyond what we can analyse theoretically, we extensively study this aspect empirically.

Momentum in Reinforcement Learning

We adapt the optimization's concept of momentum to reinforcement learning. Seeing the state-action value functions as an analog to the gradients in optimization, we interpret momentum as an average of consecutive $q$-functions. We derive Momentum Value Iteration (MoVI), a variation of Value Iteration that incorporates this momentum idea. Our analysis shows that this allows MoVI to average errors over successive iterations. We show that the proposed approach can be readily extended to deep learning. Specifically, we propose a simple improvement on DQN based on MoVI, and experiment it on Atari games.

A Theory of Regularized Markov Decision Processes

Many recent successful (deep) reinforcement learning algorithms make use of regularization, generally based on entropy or on Kullback-Leibler divergence. We propose a general theory of regularized Markov Decision Processes that generalizes these approaches in two directions: we consider a larger class of regularizers, and we consider the general modified policy iteration approach, encompassing both policy iteration and value iteration. The core building blocks of this theory are a notion of regularized Bellman operator and the Legendre-Fenchel transform, a classical tool of convex optimization. This approach allows for error propagation analyses of general algorithmic schemes of which (possibly variants of) classical algorithms such as Trust Region Policy Optimization, Soft Q-learning, Stochastic Actor Critic or Dynamic Policy Programming are special cases. This also draws connections to proximal convex optimization, especially to Mirror Descent.

Anderson Acceleration for Reinforcement Learning

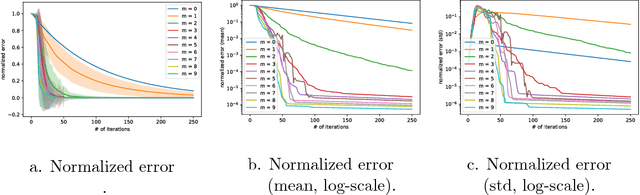
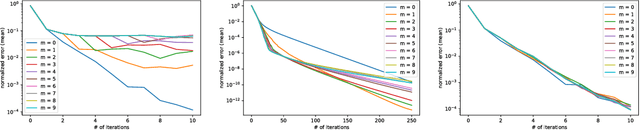
Anderson acceleration is an old and simple method for accelerating the computation of a fixed point. However, as far as we know and quite surprisingly, it has never been applied to dynamic programming or reinforcement learning. In this paper, we explain briefly what Anderson acceleration is and how it can be applied to value iteration, this being supported by preliminary experiments showing a significant speed up of convergence, that we critically discuss. We also discuss how this idea could be applied more generally to (deep) reinforcement learning.

Multiple-Step Greedy Policies in Online and Approximate Reinforcement Learning

Multiple-step lookahead policies have demonstrated high empirical competence in Reinforcement Learning, via the use of Monte Carlo Tree Search or Model Predictive Control. In a recent work \cite{efroni2018beyond}, multiple-step greedy policies and their use in vanilla Policy Iteration algorithms were proposed and analyzed. In this work, we study multiple-step greedy algorithms in more practical setups. We begin by highlighting a counter-intuitive difficulty, arising with soft-policy updates: even in the absence of approximations, and contrary to the 1-step-greedy case, monotonic policy improvement is not guaranteed unless the update stepsize is sufficiently large. Taking particular care about this difficulty, we formulate and analyze online and approximate algorithms that use such a multi-step greedy operator.

How to Combine Tree-Search Methods in Reinforcement Learning

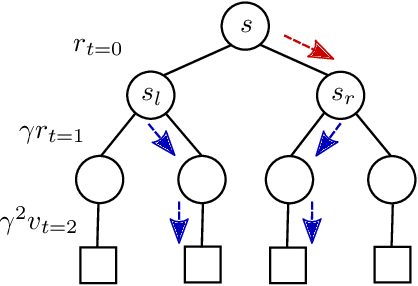
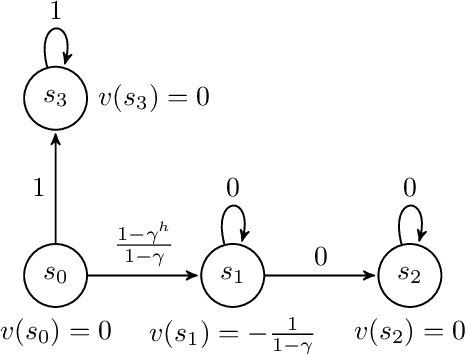
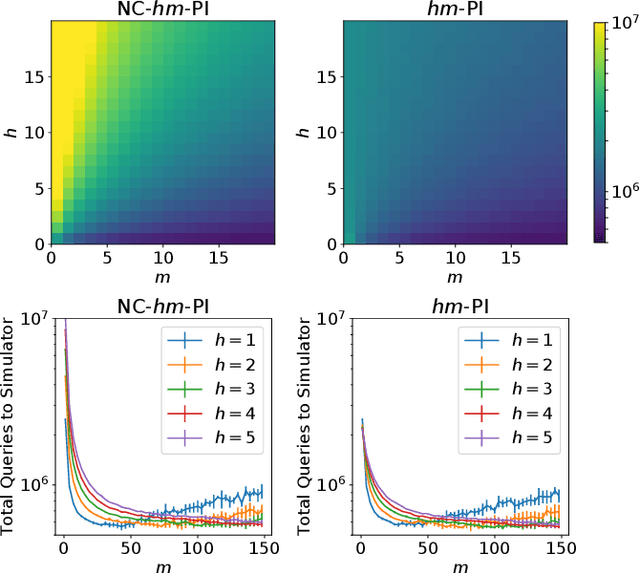
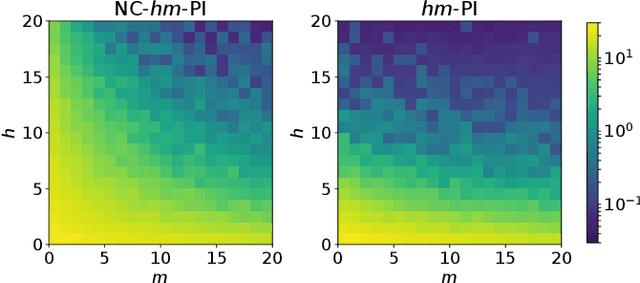
Finite-horizon lookahead policies are abundantly used in Reinforcement Learning and demonstrate impressive empirical success. Usually, the lookahead policies are implemented with specific planning methods such as Monte Carlo Tree Search (e.g. in AlphaZero). Referring to the planning problem as tree search, a reasonable practice in these implementations is to back up the value only at the leaves while the information obtained at the root is not leveraged other than for updating the policy. Here, we question the potency of this approach.Namely, the latter procedure is non-contractive in general, and its convergence is not guaranteed. Our proposed enhancement is straightforward and simple: use the return from the optimal tree path to back up the values at the descendants of the root. This leads to a \gamma^h-contracting procedure, where \gamma is the discount factor and $h$ is the tree depth. To establish our results, we first introduce a notion called multiple-step greedy consistency. We then provide convergence rates for two algorithmic instantiations of the above enhancement in the presence of noise injected to both the tree search stage and value estimation stage.

Beyond the One Step Greedy Approach in Reinforcement Learning

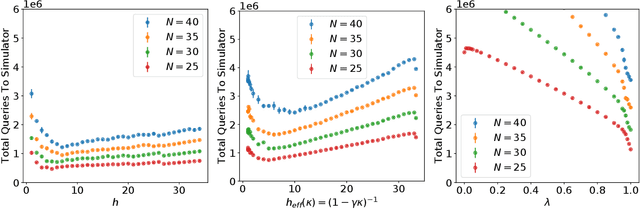
The famous Policy Iteration algorithm alternates between policy improvement and policy evaluation. Implementations of this algorithm with several variants of the latter evaluation stage, e.g, $n$-step and trace-based returns, have been analyzed in previous works. However, the case of multiple-step lookahead policy improvement, despite the recent increase in empirical evidence of its strength, has to our knowledge not been carefully analyzed yet. In this work, we introduce the first such analysis. Namely, we formulate variants of multiple-step policy improvement, derive new algorithms using these definitions and prove their convergence. Moreover, we show that recent prominent Reinforcement Learning algorithms are, in fact, instances of our framework. We thus shed light on their empirical success and give a recipe for deriving new algorithms for future study.

Improved and Generalized Upper Bounds on the Complexity of Policy Iteration

Given a Markov Decision Process (MDP) with $n$ states and a totalnumber $m$ of actions, we study the number of iterations needed byPolicy Iteration (PI) algorithms to converge to the optimal$\gamma$-discounted policy. We consider two variations of PI: Howard'sPI that changes the actions in all states with a positive advantage,and Simplex-PI that only changes the action in the state with maximaladvantage. We show that Howard's PI terminates after at most $O\left(\frac{m}{1-\gamma}\log\left(\frac{1}{1-\gamma}\right)\right)$iterations, improving by a factor $O(\log n)$ a result by Hansen etal., while Simplex-PI terminates after at most $O\left(\frac{nm}{1-\gamma}\log\left(\frac{1}{1-\gamma}\right)\right)$iterations, improving by a factor $O(\log n)$ a result by Ye. Undersome structural properties of the MDP, we then consider bounds thatare independent of the discount factor~$\gamma$: quantities ofinterest are bounds $\tau\_t$ and $\tau\_r$---uniform on all states andpolicies---respectively on the \emph{expected time spent in transientstates} and \emph{the inverse of the frequency of visits in recurrentstates} given that the process starts from the uniform distribution.Indeed, we show that Simplex-PI terminates after at most $\tilde O\left(n^3 m^2 \tau\_t \tau\_r \right)$ iterations. This extends arecent result for deterministic MDPs by Post & Ye, in which $\tau\_t\le 1$ and $\tau\_r \le n$, in particular it shows that Simplex-PI isstrongly polynomial for a much larger class of MDPs. We explain whysimilar results seem hard to derive for Howard's PI. Finally, underthe additional (restrictive) assumption that the state space ispartitioned in two sets, respectively states that are transient andrecurrent for all policies, we show that both Howard's PI andSimplex-PI terminate after at most $\tilde O(m(n^2\tau\_t+n\tau\_r))$iterations.

Rate of Convergence and Error Bounds for LSTD

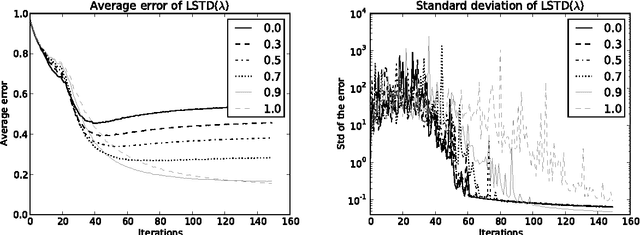
We consider LSTD($\lambda$), the least-squares temporal-difference algorithm with eligibility traces algorithm proposed by Boyan (2002). It computes a linear approximation of the value function of a fixed policy in a large Markov Decision Process. Under a $\beta$-mixing assumption, we derive, for any value of $\lambda \in (0,1)$, a high-probability estimate of the rate of convergence of this algorithm to its limit. We deduce a high-probability bound on the error of this algorithm, that extends (and slightly improves) that derived by Lazaric et al. (2012) in the specific case where $\lambda=0$. In particular, our analysis sheds some light on the choice of $\lambda$ with respect to the quality of the chosen linear space and the number of samples, that complies with simulations.