Rate of Convergence and Error Bounds for LSTD
Paper and Code
May 13, 2014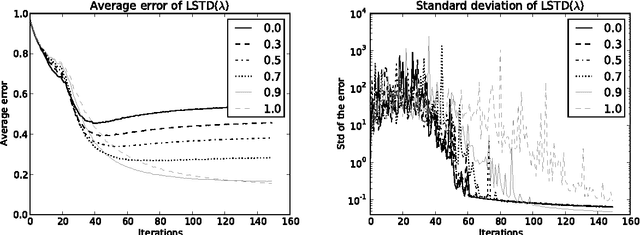
We consider LSTD($\lambda$), the least-squares temporal-difference algorithm with eligibility traces algorithm proposed by Boyan (2002). It computes a linear approximation of the value function of a fixed policy in a large Markov Decision Process. Under a $\beta$-mixing assumption, we derive, for any value of $\lambda \in (0,1)$, a high-probability estimate of the rate of convergence of this algorithm to its limit. We deduce a high-probability bound on the error of this algorithm, that extends (and slightly improves) that derived by Lazaric et al. (2012) in the specific case where $\lambda=0$. In particular, our analysis sheds some light on the choice of $\lambda$ with respect to the quality of the chosen linear space and the number of samples, that complies with simulations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge