Leverage the Average: an Analysis of Regularization in RL

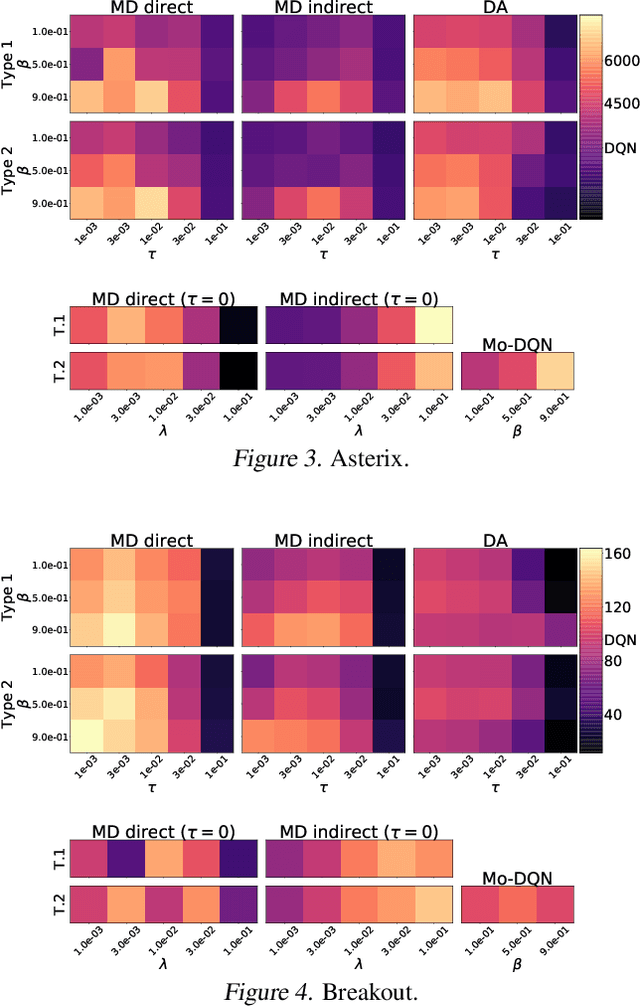
Building upon the formalism of regularized Markov decision processes, we study the effect of Kullback-Leibler (KL) and entropy regularization in reinforcement learning. Through an equivalent formulation of the related approximate dynamic programming (ADP) scheme, we show that a KL penalty amounts to averaging q-values. This equivalence allows drawing connections between a priori disconnected methods from the literature, and proving that a KL regularization indeed leads to averaging errors made at each iteration of value function update. With the proposed theoretical analysis, we also study the interplay between KL and entropy regularization. When the considered ADP scheme is combined with neural-network-based stochastic approximations, the equivalence is lost, which suggests a number of different ways to do regularization. Because this goes beyond what we can analyse theoretically, we extensively study this aspect empirically.