Topology guaranteed segmentation of the human retina from OCT using convolutional neural networks

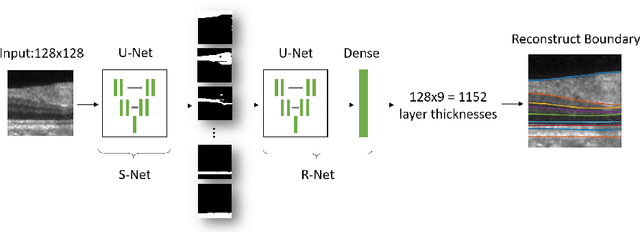
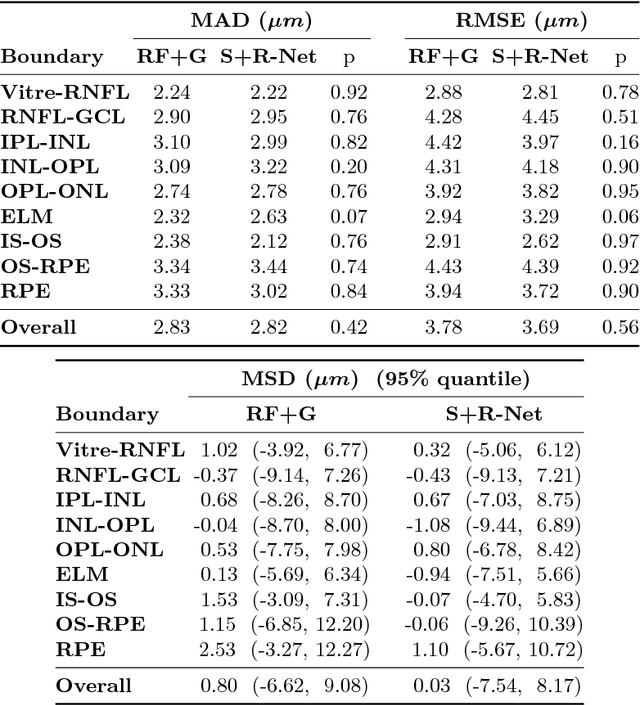
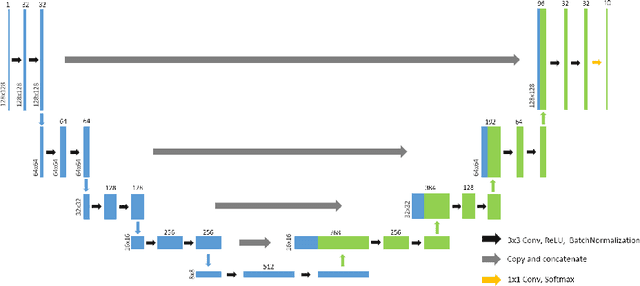
Optical coherence tomography (OCT) is a noninvasive imaging modality which can be used to obtain depth images of the retina. The changing layer thicknesses can thus be quantified by analyzing these OCT images, moreover these changes have been shown to correlate with disease progression in multiple sclerosis. Recent automated retinal layer segmentation tools use machine learning methods to perform pixel-wise labeling and graph methods to guarantee the layer hierarchy or topology. However, graph parameters like distance and smoothness constraints must be experimentally assigned by retinal region and pathology, thus degrading the flexibility and time efficiency of the whole framework. In this paper, we develop cascaded deep networks to provide a topologically correct segmentation of the retinal layers in a single feed forward propagation. The first network (S-Net) performs pixel-wise labeling and the second regression network (R-Net) takes the topologically unconstrained S-Net results and outputs layer thicknesses for each layer and each position. Relu activation is used as the final operation of the R-Net which guarantees non-negativity of the output layer thickness. Since the segmentation boundary position is acquired by summing up the corresponding non-negative layer thicknesses, the layer ordering (i.e., topology) of the reconstructed boundaries is guaranteed even at the fovea where the distances between boundaries can be zero. The R-Net is trained using simulated masks and thus can be generalized to provide topology guaranteed segmentation for other layered structures. This deep network has achieved comparable mean absolute boundary error (2.82 {\mu}m) to state-of-the-art graph methods (2.83 {\mu}m).

Probabilistic Group Testing under Sum Observations: A Parallelizable 2-Approximation for Entropy Loss

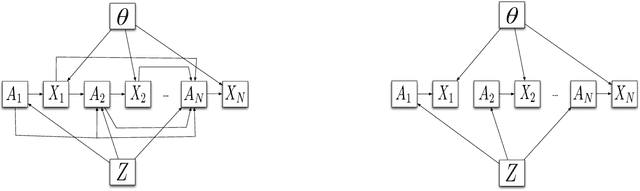
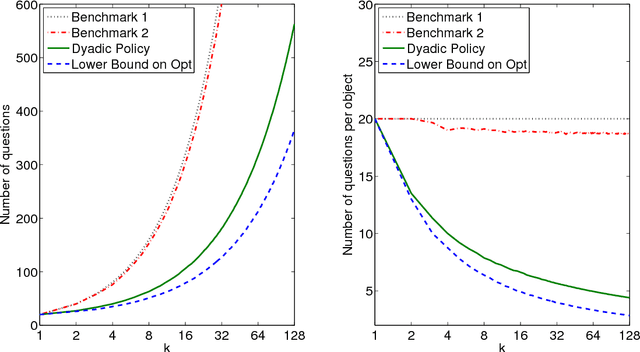
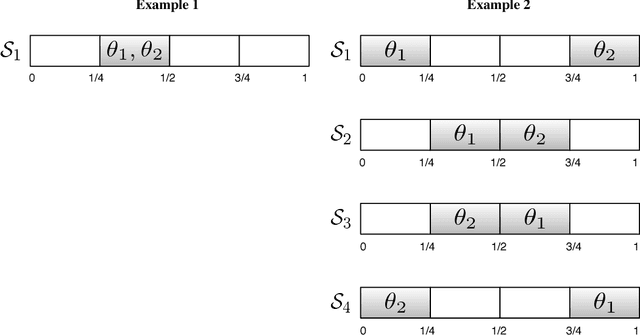
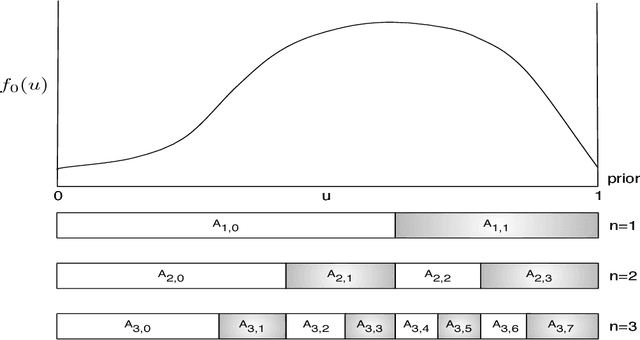
We consider the problem of group testing with sum observations and noiseless answers, in which we aim to locate multiple objects by querying the number of objects in each of a sequence of chosen sets. We study a probabilistic setting with entropy loss, in which we assume a joint Bayesian prior density on the locations of the objects and seek to choose the sets queried to minimize the expected entropy of the Bayesian posterior distribution after a fixed number of questions. We present a new non-adaptive policy, called the dyadic policy, show it is optimal among non-adaptive policies, and is within a factor of two of optimal among adaptive policies. This policy is quick to compute, its nonadaptive nature makes it easy to parallelize, and our bounds show it performs well even when compared with adaptive policies. We also study an adaptive greedy policy, which maximizes the one-step expected reduction in entropy, and show that it performs at least as well as the dyadic policy, offering greater query efficiency but reduced parallelism. Numerical experiments demonstrate that both procedures outperform a divide-and-conquer benchmark policy from the literature, called sequential bifurcation, and show how these procedures may be applied in a stylized computer vision problem.