Purnima Rajan
Probabilistic Group Testing under Sum Observations: A Parallelizable 2-Approximation for Entropy Loss
Sep 23, 2015
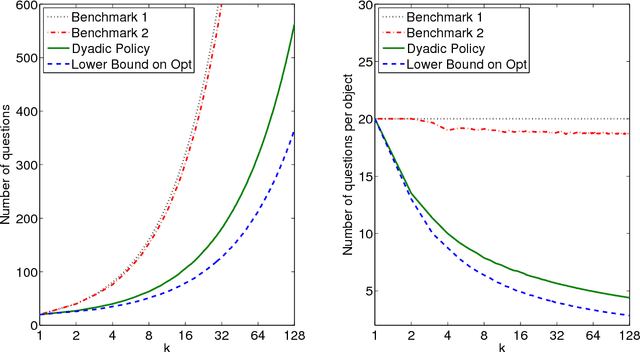
Abstract:We consider the problem of group testing with sum observations and noiseless answers, in which we aim to locate multiple objects by querying the number of objects in each of a sequence of chosen sets. We study a probabilistic setting with entropy loss, in which we assume a joint Bayesian prior density on the locations of the objects and seek to choose the sets queried to minimize the expected entropy of the Bayesian posterior distribution after a fixed number of questions. We present a new non-adaptive policy, called the dyadic policy, show it is optimal among non-adaptive policies, and is within a factor of two of optimal among adaptive policies. This policy is quick to compute, its nonadaptive nature makes it easy to parallelize, and our bounds show it performs well even when compared with adaptive policies. We also study an adaptive greedy policy, which maximizes the one-step expected reduction in entropy, and show that it performs at least as well as the dyadic policy, offering greater query efficiency but reduced parallelism. Numerical experiments demonstrate that both procedures outperform a divide-and-conquer benchmark policy from the literature, called sequential bifurcation, and show how these procedures may be applied in a stylized computer vision problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge