Efficient Batch and Recursive Least Squares for Matrix Parameter Estimation with Application to Adaptive MPC

Traditionally, batch least squares (BLS) and recursive least squares (RLS) are used for identification of a vector of parameters that form a linear model. In some situations, however, it is of interest to identify parameters in a matrix structure. In this case, a common approach is to transform the problem into standard vector form using the vectorization (vec) operator and the Kronecker product, known as vec-permutation. However, the use of the Kronecker product introduces extraneous zero terms in the regressor, resulting in unnecessary additional computational and space requirements. This work derives matrix BLS and RLS formulations which, under mild assumptions, minimize the same cost as the vec-permutation approach. This new approach requires less computational complexity and space complexity than vec-permutation in both BLS and RLS identification. It is also shown that persistent excitation guarantees convergence to the true matrix parameters. This method can used to improve computation time in the online identification of multiple-input, multiple-output systems for indirect adaptive model predictive control.

SIFt-RLS: Subspace of Information Forgetting Recursive Least Squares

This paper presents subspace of information forgetting recursive least squares (SIFt-RLS), a directional forgetting algorithm which, at each step, forgets only in row space of the regressor matrix, or the \textit{information subspace}. As a result, SIFt-RLS tracks parameters that are in excited directions while not changing parameter estimation in unexcited directions. It is shown that SIFt-RLS guarantees an upper and lower bound of the covariance matrix, without assumptions of persistent excitation, and explicit bounds are given. Furthermore, sufficient conditions are given for the uniform Lyapunov stability and global uniform exponential stability of parameter estimation error in SIFt-RLS when estimating fixed parameters without noise. SIFt-RLS is compared to other RLS algorithms from the literature in a numerical example without persistently exciting data.

Convergence of Recursive Least Squares Based Input/Output System Identification with Model Order Mismatch

Discrete-time input/output models, also called infinite impulse response (IIR) models or autoregressive moving average (ARMA) models, are useful for online identification as they can be efficiently updated using recursive least squares (RLS) as new data is collected. Several works have studied the convergence of the input/output model coefficients identified using RLS under the assumption that the order of the identified model is the same as that of the true system. However, the case of model order mismatch is not as well addressed. This work begins by introducing the notion of \textit{equivalence} of input/output models of different orders. Next, this work analyzes online identification of input/output models in the case where the order of the identified model is higher than that of the true system. It is shown that, given persistently exciting data, the higher-order identified model converges to the model equivalent to the true system that minimizes the regularization term of RLS.

Adaptive Kalman Filtering Developed from Recursive Least Squares Forgetting Algorithms

Recursive least squares (RLS) is derived as the recursive minimizer of the least-squares cost function. Moreover, it is well known that RLS is a special case of the Kalman filter. This work presents the Kalman filter least squares (KFLS) cost function, whose recursive minimizer gives the Kalman filter. KFLS is an extension of generalized forgetting recursive least squares (GF-RLS), a general framework which contains various extensions of RLS from the literature as special cases. This then implies that extensions of RLS are also special cases of the Kalman filter. Motivated by this connection, we propose an algorithm that combines extensions of RLS with the Kalman filter, resulting in a new class of adaptive Kalman filters. A numerical example shows that one such adaptive Kalman filter provides improved state estimation for a mass-spring-damper with intermittent, unmodeled collisions. This example suggests that such adaptive Kalman filtering may provide potential benefits for systems with non-classical disturbances.

Adaptive Real-Time Numerical Differentiation with Variable-Rate Forgetting and Exponential Resetting

Digital PID control requires a differencing operation to implement the D gain. In order to suppress the effects of noisy data, the traditional approach is to filter the data, where the frequency response of the filter is adjusted manually based on the characteristics of the sensor noise. The present paper considers the case where the characteristics of the sensor noise change over time in an unknown way. This problem is addressed by applying adaptive real-time numerical differentiation based on adaptive input and state estimation (AISE). The contribution of this paper is to extend AISE to include variable-rate forgetting with exponential resetting, which allows AISE to more rapidly respond to changing noise characteristics while enforcing the boundedness of the covariance matrix used in recursive least squares.

Generalized Forgetting Recursive Least Squares: Stability and Robustness Guarantees

This work present generalized forgetting recursive least squares (GF-RLS), a generalization of recursive least squares (RLS) that encompasses many extensions of RLS as special cases. First, sufficient conditions are presented for the 1) Lyapunov stability, 2) uniform Lyapunov stability, 3) global asymptotic stability, and 4) global uniform exponential stability of parameter estimation error in GF-RLS when estimating fixed parameters without noise. Second, robustness guarantees are derived for the estimation of time-varying parameters in the presence of measurement noise and regressor noise. These robustness guarantees are presented in terms of global uniform ultimate boundedness of the parameter estimation error. A specialization of this result gives a bound to the asymptotic bias of least squares estimators in the errors-in-variables problem. Lastly, a survey is presented to show how GF-RLS can be used to analyze various extensions of RLS from the literature.

Time-Supervised Primary Object Segmentation

We describe an unsupervised method to detect and segment portions of live scenes that, at some point in time, are seen moving as a coherent whole, which we refer to as primary objects. Our method first segments motions by minimizing the mutual information between partitions of the image domain, which bootstraps a static object detection model that takes a single image as input. The two models are mutually reinforced within a feedback loop, enabling extrapolation to previously unseen classes of objects. Our method requires video for training, but can be used on either static images or videos at inference time. As the volume of our training sets grows, more and more objects are seen moving, thus turning our method into unsupervised (or time-supervised) training to segment primary objects. The resulting system outperforms the state-of-the-art in both video object segmentation and salient object detection benchmarks, even when compared to methods that use explicit manual annotation.

ErrorNet: Learning error representations from limited data to improve vascular segmentation

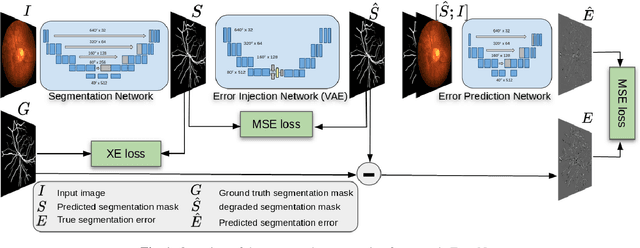
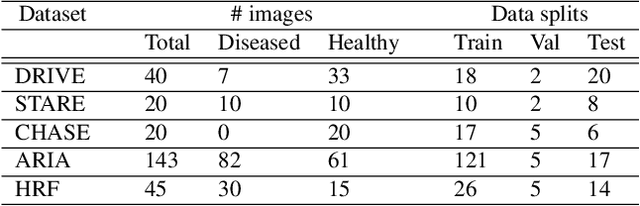
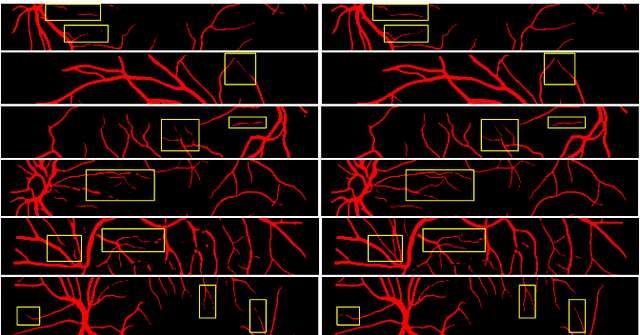
Deep convolutional neural networks have proved effective in segmenting lesions and anatomies in various medical imaging modalities. However, in the presence of small sample size and domain shift problems, these models often produce masks with non-intuitive segmentation mistakes. In this paper, we propose a segmentation framework called ErrorNet, which learns to correct these segmentation mistakes through the repeated process of injecting systematic segmentation errors to a segmentation mask based on a learned shape prior, followed by attempting to predict the injected error. During inference, ErrorNet corrects the segmentation mistakes by adding the predicted error map to the initial segmentation mask. ErrorNet has advantages over alternatives based on domain adaptation or CRF-based post processing, because it requires neither domain-specific parameter tuning nor any data from the target domains. We have evaluated ErrorNet using five public datasets for the task of retinal vessel segmentation. The selected datasets differ in size and patient population, allowing us to evaluate the effectiveness of ErrorNet in handling small sample size and domain shift problems. Our experiments demonstrate that ErrorNet outperforms a base segmentation model, a CRF-based post processing scheme, and a domain adaptation method, with a greater performance gain in the presence of dataset limitations above.