Target Tracking Using the Invariant Extended Kalman Filter with Numerical Differentiation for Estimating Curvature and Torsion

The goal of target tracking is to estimate target position, velocity, and acceleration in real time using position data. This paper introduces a novel target-tracking technique that uses adaptive input and state estimation (AISE) for real-time numerical differentiation to estimate velocity, acceleration, and jerk from position data. These estimates are used to model the target motion within the Frenet-Serret (FS) frame. By representing the model in SE(3), the position and velocity are estimated using the invariant extended Kalman filter (IEKF). The proposed method, called FS-IEKF-AISE, is illustrated by numerical examples and compared to prior techniques.

Frenet-Serret-Based Trajectory Prediction

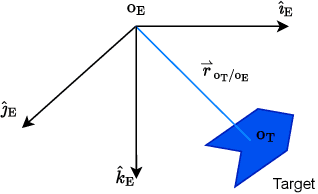
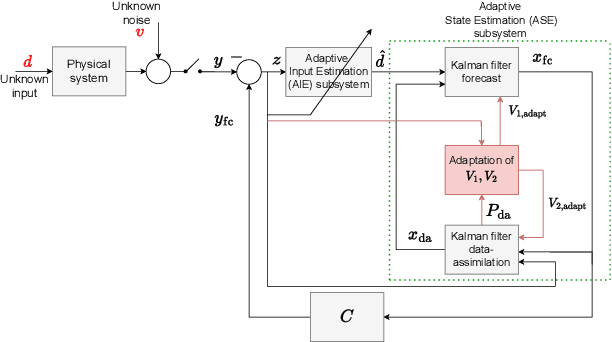
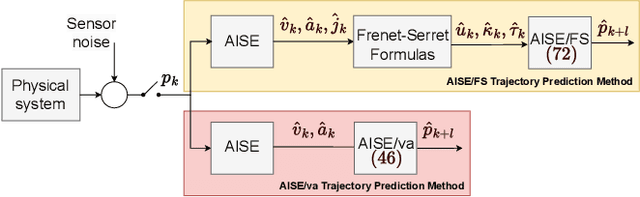
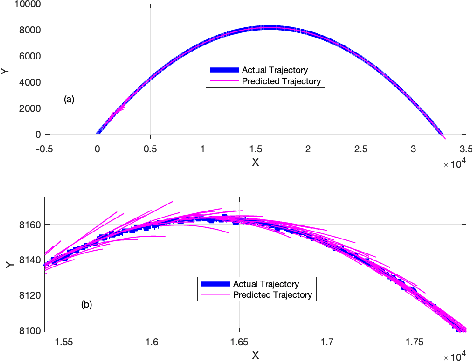
Trajectory prediction is a crucial element of guidance, navigation, and control systems. This paper presents two novel trajectory-prediction methods based on real-time position measurements and adaptive input and state estimation (AISE). The first method, called AISE/va, uses position measurements to estimate the target velocity and acceleration. The second method, called AISE/FS, models the target trajectory as a 3D curve using the Frenet-Serret formulas, which require estimates of velocity, acceleration, and jerk. To estimate velocity, acceleration, and jerk in real time, AISE computes first, second, and third derivatives of the position measurements. AISE does not rely on assumptions about the target maneuver, measurement noise, or disturbances. For trajectory prediction, both methods use measurements of the target position and estimates of its derivatives to extrapolate from the current position. The performance of AISE/va and AISE/FS is compared numerically with the $\alpha$-$\beta$-$\gamma$ filter, which shows that AISE/FS provides more accurate trajectory prediction than AISE/va and traditional methods, especially for complex target maneuvers.

Recursive Least Squares with Fading Regularization for Finite-Time Convergence without Persistent Excitation

This paper extends recursive least squares (RLS) to include time-varying regularization. This extension provides flexibility for updating the least squares regularization term in real time. Existing results with constant regularization imply that the parameter-estimation error dynamics of RLS are globally attractive to zero if and only the regressor is weakly persistently exciting. This work shows that, by extending classical RLS to include a time-varying (fading) regularization term that converges to zero, the parameter-estimation error dynamics are globally attractive to zero without weakly persistent excitation. Moreover, if the fading regularization term converges to zero in finite time, then the parameter estimation error also converges to zero in finite time. Finally, we propose rank-1 fading regularization (R1FR) RLS, a time-varying regularization algorithm with fading regularization that converges to zero, and which runs in the same computational complexity as classical RLS. Numerical examples are presented to validate theoretical guarantees and to show how R1FR-RLS can protect against over-regularization.

Convergence of Recursive Least Squares Based Input/Output System Identification with Model Order Mismatch

Discrete-time input/output models, also called infinite impulse response (IIR) models or autoregressive moving average (ARMA) models, are useful for online identification as they can be efficiently updated using recursive least squares (RLS) as new data is collected. Several works have studied the convergence of the input/output model coefficients identified using RLS under the assumption that the order of the identified model is the same as that of the true system. However, the case of model order mismatch is not as well addressed. This work begins by introducing the notion of \textit{equivalence} of input/output models of different orders. Next, this work analyzes online identification of input/output models in the case where the order of the identified model is higher than that of the true system. It is shown that, given persistently exciting data, the higher-order identified model converges to the model equivalent to the true system that minimizes the regularization term of RLS.

Efficient Batch and Recursive Least Squares for Matrix Parameter Estimation with Application to Adaptive MPC

Traditionally, batch least squares (BLS) and recursive least squares (RLS) are used for identification of a vector of parameters that form a linear model. In some situations, however, it is of interest to identify parameters in a matrix structure. In this case, a common approach is to transform the problem into standard vector form using the vectorization (vec) operator and the Kronecker product, known as vec-permutation. However, the use of the Kronecker product introduces extraneous zero terms in the regressor, resulting in unnecessary additional computational and space requirements. This work derives matrix BLS and RLS formulations which, under mild assumptions, minimize the same cost as the vec-permutation approach. This new approach requires less computational complexity and space complexity than vec-permutation in both BLS and RLS identification. It is also shown that persistent excitation guarantees convergence to the true matrix parameters. This method can used to improve computation time in the online identification of multiple-input, multiple-output systems for indirect adaptive model predictive control.

SIFt-RLS: Subspace of Information Forgetting Recursive Least Squares

This paper presents subspace of information forgetting recursive least squares (SIFt-RLS), a directional forgetting algorithm which, at each step, forgets only in row space of the regressor matrix, or the \textit{information subspace}. As a result, SIFt-RLS tracks parameters that are in excited directions while not changing parameter estimation in unexcited directions. It is shown that SIFt-RLS guarantees an upper and lower bound of the covariance matrix, without assumptions of persistent excitation, and explicit bounds are given. Furthermore, sufficient conditions are given for the uniform Lyapunov stability and global uniform exponential stability of parameter estimation error in SIFt-RLS when estimating fixed parameters without noise. SIFt-RLS is compared to other RLS algorithms from the literature in a numerical example without persistently exciting data.

Adaptive Kalman Filtering Developed from Recursive Least Squares Forgetting Algorithms

Recursive least squares (RLS) is derived as the recursive minimizer of the least-squares cost function. Moreover, it is well known that RLS is a special case of the Kalman filter. This work presents the Kalman filter least squares (KFLS) cost function, whose recursive minimizer gives the Kalman filter. KFLS is an extension of generalized forgetting recursive least squares (GF-RLS), a general framework which contains various extensions of RLS from the literature as special cases. This then implies that extensions of RLS are also special cases of the Kalman filter. Motivated by this connection, we propose an algorithm that combines extensions of RLS with the Kalman filter, resulting in a new class of adaptive Kalman filters. A numerical example shows that one such adaptive Kalman filter provides improved state estimation for a mass-spring-damper with intermittent, unmodeled collisions. This example suggests that such adaptive Kalman filtering may provide potential benefits for systems with non-classical disturbances.

A Data-Driven Autopilot for Fixed-Wing Aircraft Based on Model Predictive Control

Autopilots for fixed-wing aircraft are typically designed based on linearized aerodynamic models consisting of stability and control derivatives obtained from wind-tunnel testing. The resulting local controllers are then pieced together using gain scheduling. For applications in which the aerodynamics are unmodeled, the present paper proposes an autopilot based on predictive cost adaptive control (PCAC). As an indirect adaptive control extension of model predictive control, PCAC uses recursive least squares (RLS) with variable-rate forgetting for online, closed-loop system identification. At each time step, RLS-based system identification updates the coefficients of an input-output model whose order is a hyperparameter specified by the user. For MPC, the receding-horizon optimization can be performed by either the backward-propagating Riccati equation or quadratic programming. The present paper investigates the performance of PCAC for fixed-wing aircraft without the use of any aerodynamic modeling or offline/prior data collection.

Adaptive Real-Time Numerical Differentiation with Variable-Rate Forgetting and Exponential Resetting

Digital PID control requires a differencing operation to implement the D gain. In order to suppress the effects of noisy data, the traditional approach is to filter the data, where the frequency response of the filter is adjusted manually based on the characteristics of the sensor noise. The present paper considers the case where the characteristics of the sensor noise change over time in an unknown way. This problem is addressed by applying adaptive real-time numerical differentiation based on adaptive input and state estimation (AISE). The contribution of this paper is to extend AISE to include variable-rate forgetting with exponential resetting, which allows AISE to more rapidly respond to changing noise characteristics while enforcing the boundedness of the covariance matrix used in recursive least squares.

Kinematics-Based Sensor Fault Detection for Autonomous Vehicles Using Real-Time Numerical Differentiation

Sensor fault detection is of extreme importance for ensuring the safe operation of vehicles. This paper introduces a novel approach to detecting and identifying faulty sensors. For ground vehicles confined to the horizontal plane, this technique is based on six kinematics-based error metrics that are computed in real time by using onboard sensor data encompassing compass, radar, rate gyro, and accelerometer measurements as well as their derivatives. Real-time numerical differentiation is performed by applying the adaptive input and state estimation (AIE/ASE) algorithm. Numerical examples are provided to assess the efficacy of the proposed methodology.