Efficient Extrinsic Calibration of Multi-Sensor 3D LiDAR Systems for Autonomous Vehicles using Static Objects Information

For an autonomous vehicle, the ability to sense its surroundings and to build an overall representation of the environment by fusing different sensor data streams is fundamental. To this end, the poses of all sensors need to be accurately determined. Traditional calibration methods are based on: 1) using targets specifically designed for calibration purposes in controlled environments, 2) optimizing a quality metric of the point clouds collected while traversing an unknown but static environment, or 3) optimizing the match among per-sensor incremental motion observations along a motion path fulfilling special requirements. In real scenarios, however, the online applicability of these methods can be limited, as they are typically highly dynamic, contain degenerate paths, and require fast computations. In this paper, we propose an approach that tackles some of these challenges by formulating the calibration problem as a joint but structured optimization problem of all sensor calibrations that takes as input a summary of the point cloud information consisting of ground points and pole detections. We demonstrate the efficiency and quality of the results of the proposed approach in a set of experiments with LiDAR simulation and real data from an urban trip.

Efficient Multi-Contact Pattern Generation with Sequential Convex Approximations of the Centroidal Dynamics

This paper investigates the problem of efficient computation of physically consistent multi-contact behaviors. Recent work showed that under mild assumptions, the problem could be decomposed into simpler kinematic and centroidal dynamic optimization problems. Based on this approach, we propose a general convex relaxation of the centroidal dynamics leading to two computationally efficient algorithms based on iterative resolutions of second order cone programs. They optimize centroidal trajectories, contact forces and, importantly, the timing of the motions. We include the approach in a kino-dynamic optimization method to generate full-body movements. Finally, the approach is embedded in a mixed-integer solver to further find dynamically consistent contact sequences. Extensive numerical experiments demonstrate the computational efficiency of the approach, suggesting that it could be used in a fast receding horizon control loop. Executions of the planned motions on simulated humanoids and quadrupeds and on a real quadruped robot further show the quality of the optimized motions.

Efficient Humanoid Contact Planning using Learned Centroidal Dynamics Prediction

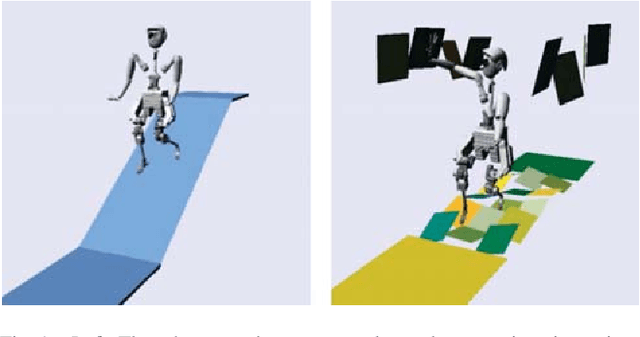
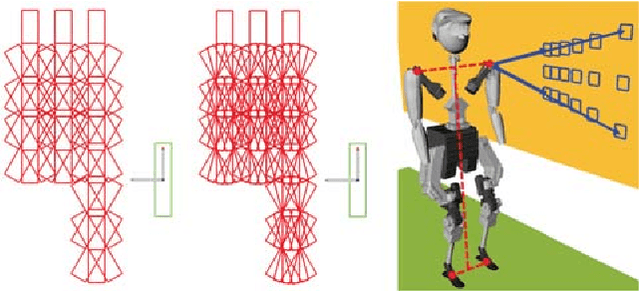
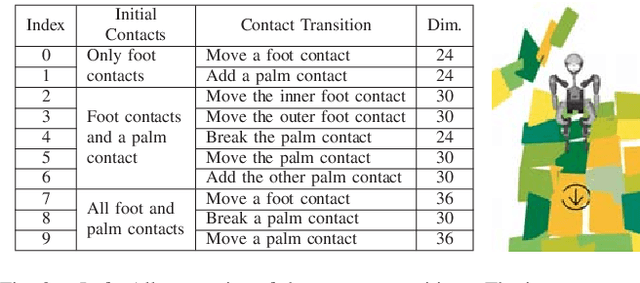
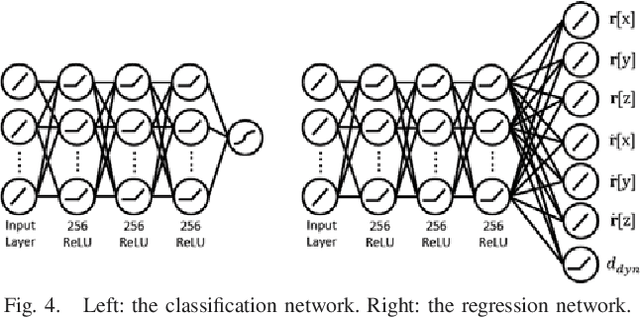
Humanoid robots dynamically navigate an environment by interacting with it via contact wrenches exerted at intermittent contact poses. Therefore, it is important to consider dynamics when planning a contact sequence. Traditional contact planning approaches assume a quasi-static balance criterion to reduce the computational challenges of selecting a contact sequence over a rough terrain. This however limits the applicability of the approach when dynamic motions are required, such as when walking down a steep slope or crossing a wide gap. Recent methods overcome this limitation with the help of efficient mixed integer convex programming solvers capable of synthesizing dynamic contact sequences. Nevertheless, its exponential-time complexity limits its applicability to short time horizon contact sequences within small environments. In this paper, we go beyond current approaches by learning a prediction of the dynamic evolution of the robot centroidal momenta, which can then be used for quickly generating dynamically robust contact sequences for robots with arms and legs using a search-based contact planner. We demonstrate the efficiency and quality of the results of the proposed approach in a set of dynamically challenging scenarios.

On Time Optimization of Centroidal Momentum Dynamics

Recently, the centroidal momentum dynamics has received substantial attention to plan dynamically consistent motions for robots with arms and legs in multi-contact scenarios. However, it is also non convex which renders any optimization approach difficult and timing is usually kept fixed in most trajectory optimization techniques to not introduce additional non convexities to the problem. But this can limit the versatility of the algorithms. In our previous work, we proposed a convex relaxation of the problem that allowed to efficiently compute momentum trajectories and contact forces. However, our approach could not minimize a desired angular momentum objective which seriously limited its applicability. Noticing that the non-convexity introduced by the time variables is of similar nature as the centroidal dynamics one, we propose two convex relaxations to the problem based on trust regions and soft constraints. The resulting approaches can compute time-optimized dynamically consistent trajectories sufficiently fast to make the approach realtime capable. The performance of the algorithm is demonstrated in several multi-contact scenarios for a humanoid robot. In particular, we show that the proposed convex relaxation of the original problem finds solutions that are consistent with the original non-convex problem and illustrate how timing optimization allows to find motion plans that would be difficult to plan with fixed timing.

The Role of Measurement Uncertainty in Optimal Control for Contact Interactions

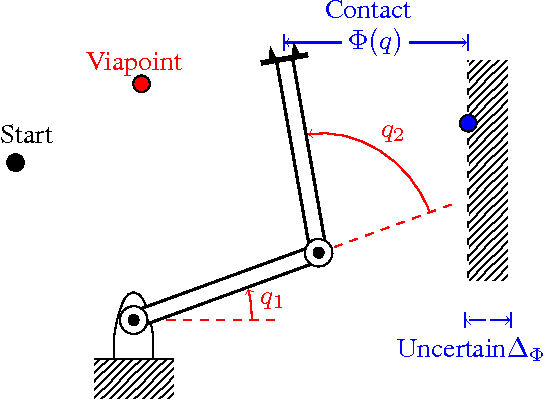
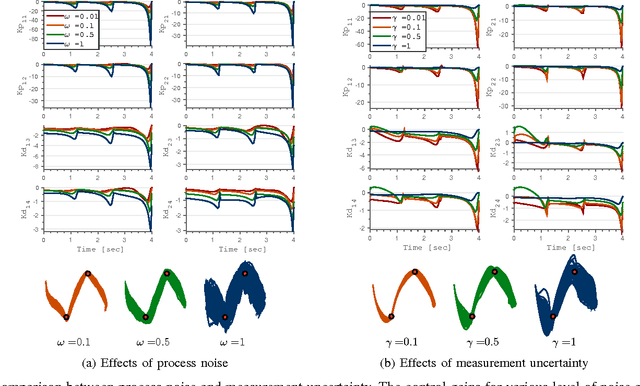
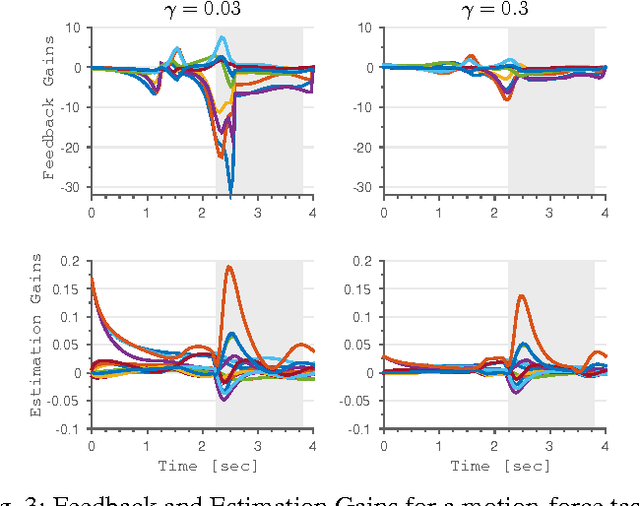
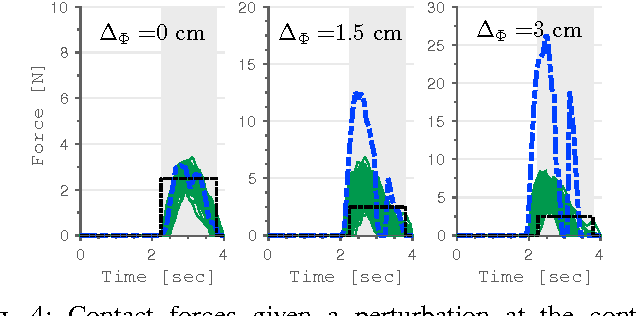
Stochastic Optimal Control (SOC) typically considers noise only in the process model, i.e. unknown disturbances. However, in many robotic applications that involve interaction with the environment, such as locomotion and manipulation, uncertainty also comes from lack of precise knowledge of the world, which is not an actual disturbance. We develop a computationally efficient SOC algorithm, based on risk-sensitive control, that takes into account uncertainty in the measurements. We include the dynamics of an observer in such a way that the control law explicitly depends on the current measurement uncertainty. We show that high measurement uncertainty leads to low impedance behaviors, a result in contrast with the effects of process noise variance that creates stiff behaviors. Simulation results on a simple 2D manipulator show that our controller can create better interaction with the environment under uncertain contact locations than traditional SOC approaches.

A Convex Model of Momentum Dynamics for Multi-Contact Motion Generation

Linear models for control and motion generation of humanoid robots have received significant attention in the past years, not only due to their well known theoretical guarantees, but also because of practical computational advantages. However, to tackle more challenging tasks and scenarios such as locomotion on uneven terrain, a more expressive model is required. In this paper, we are interested in contact interaction-centered motion optimization based on the momentum dynamics model. This model is non-linear and non-convex; however, we find a relaxation of the problem that allows us to formulate it as a single convex quadratically-constrained quadratic program (QCQP) that can be very efficiently optimized. Furthermore, experimental results suggest that this relaxation is tight and therefore useful for multi-contact planning. This convex model is then coupled to the optimization of end-effector contacts location using a mixed integer program, which can be solved in realtime. This becomes relevant e.g. to recover from external pushes, where a predefined stepping plan is likely to fail and an online adaptation of the contact location is needed. The performance of our algorithm is demonstrated in several multi-contact scenarios for humanoid robot.