Deep Active Learning based Experimental Design to Uncover Synergistic Genetic Interactions for Host Targeted Therapeutics

Recent technological advances have introduced new high-throughput methods for studying host-virus interactions, but testing synergistic interactions between host gene pairs during infection remains relatively slow and labor intensive. Identification of multiple gene knockdowns that effectively inhibit viral replication requires a search over the combinatorial space of all possible target gene pairs and is infeasible via brute-force experiments. Although active learning methods for sequential experimental design have shown promise, existing approaches have generally been restricted to single-gene knockdowns or small-scale double knockdown datasets. In this study, we present an integrated Deep Active Learning (DeepAL) framework that incorporates information from a biological knowledge graph (SPOKE, the Scalable Precision Medicine Open Knowledge Engine) to efficiently search the configuration space of a large dataset of all pairwise knockdowns of 356 human genes in HIV infection. Through graph representation learning, the framework is able to generate task-specific representations of genes while also balancing the exploration-exploitation trade-off to pinpoint highly effective double-knockdown pairs. We additionally present an ensemble method for uncertainty quantification and an interpretation of the gene pairs selected by our algorithm via pathway analysis. To our knowledge, this is the first work to show promising results on double-gene knockdown experimental data of appreciable scale (356 by 356 matrix).

Nonstationary Multivariate Gaussian Processes for Electronic Health Records

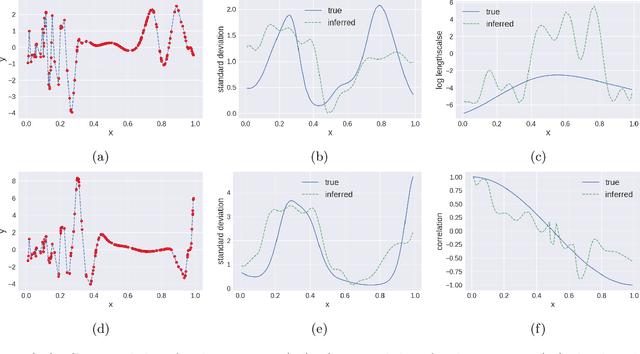
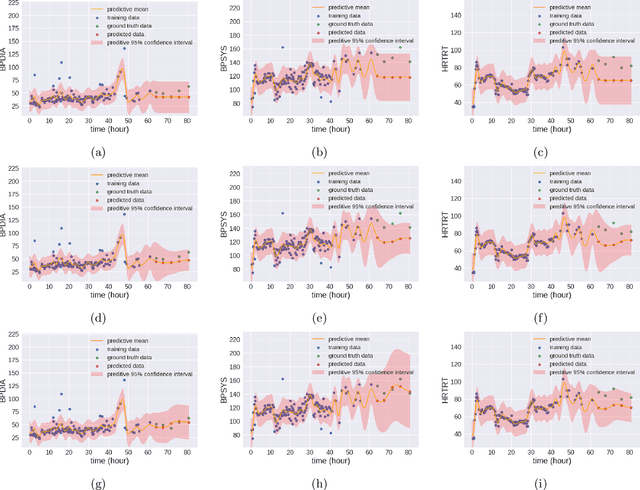
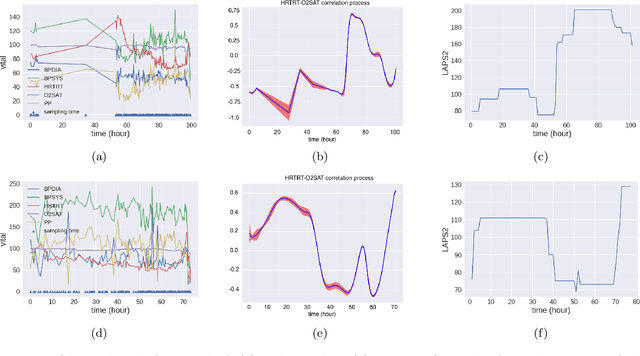
We propose multivariate nonstationary Gaussian processes for jointly modeling multiple clinical variables, where the key parameters, length-scales, standard deviations and the correlations between the observed output, are all time dependent. We perform posterior inference via Hamiltonian Monte Carlo (HMC). We also provide methods for obtaining computationally efficient gradient-based maximum a posteriori (MAP) estimates. We validate our model on synthetic data as well as on electronic health records (EHR) data from Kaiser Permanente (KP). We show that the proposed model provides better predictive performance over a stationary model as well as uncovers interesting latent correlation processes across vitals which are potentially predictive of patient risk.