Nonstationary Multivariate Gaussian Processes for Electronic Health Records

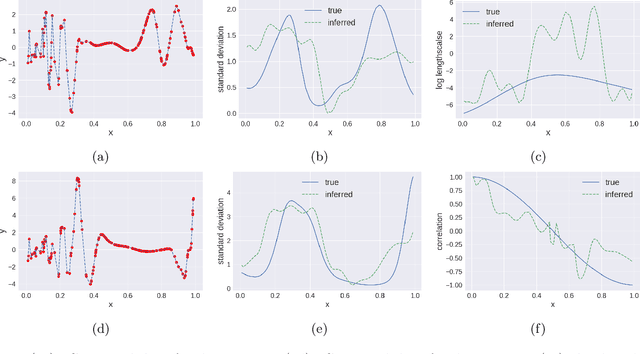
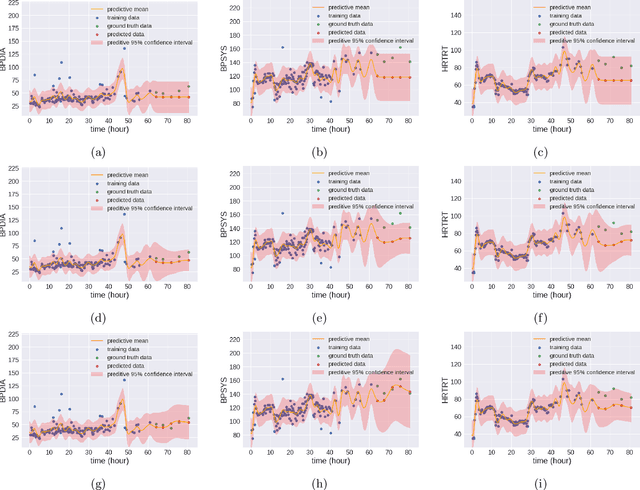
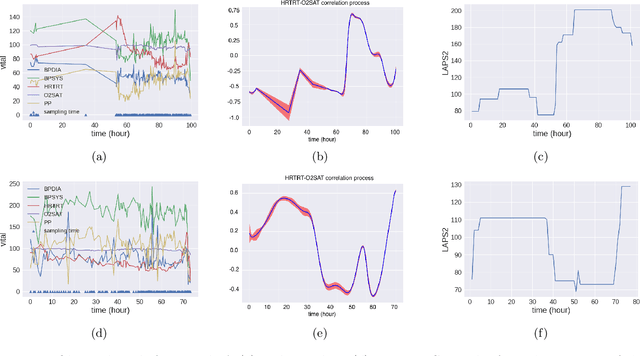
We propose multivariate nonstationary Gaussian processes for jointly modeling multiple clinical variables, where the key parameters, length-scales, standard deviations and the correlations between the observed output, are all time dependent. We perform posterior inference via Hamiltonian Monte Carlo (HMC). We also provide methods for obtaining computationally efficient gradient-based maximum a posteriori (MAP) estimates. We validate our model on synthetic data as well as on electronic health records (EHR) data from Kaiser Permanente (KP). We show that the proposed model provides better predictive performance over a stationary model as well as uncovers interesting latent correlation processes across vitals which are potentially predictive of patient risk.

Hierarchical Hidden Markov Jump Processes for Cancer Screening Modeling

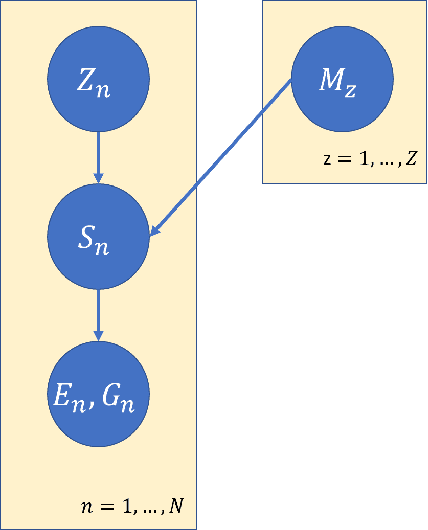
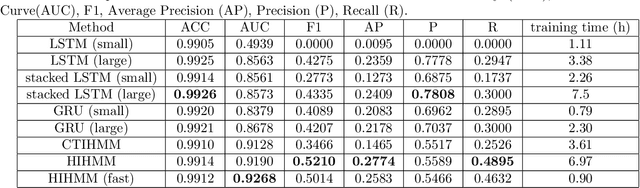
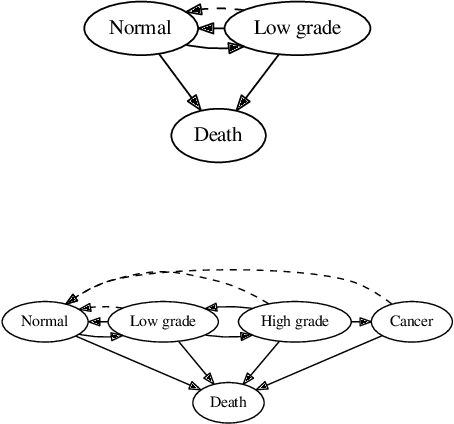
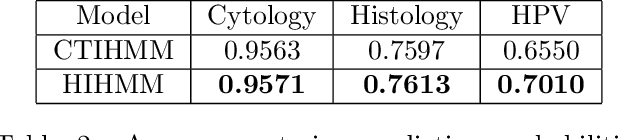
Hidden Markov jump processes are an attractive approach for modeling clinical disease progression data because they are explainable and capable of handling both irregularly sampled and noisy data. Most applications in this context consider time-homogeneous models due to their relative computational simplicity. However, the time homogeneous assumption is too strong to accurately model the natural history of many diseases. Moreover, the population at risk is not homogeneous either, since disease exposure and susceptibility can vary considerably. In this paper, we propose a piece-wise stationary transition matrix to explain the heterogeneity in time. We propose a hierarchical structure for the heterogeneity in population, where prior information is considered to deal with unbalanced data. Moreover, an efficient, scalable EM algorithm is proposed for inference. We demonstrate the feasibility and superiority of our model on a cervical cancer screening dataset from the Cancer Registry of Norway. Experiments show that our model outperforms state-of-the-art recurrent neural network models in terms of prediction accuracy and significantly outperforms a standard hidden Markov jump process in generating Kaplan-Meier estimators.

Regularized Sparse Gaussian Processes

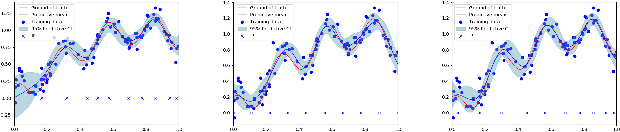
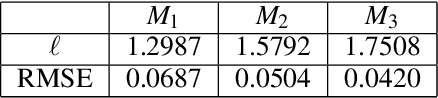
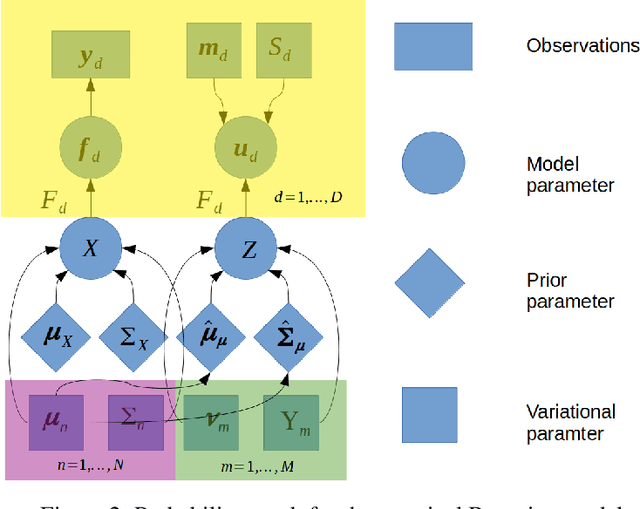
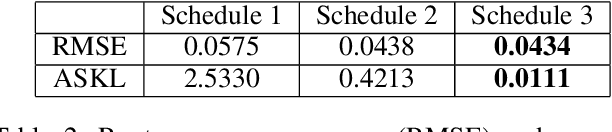
Gaussian processes are a flexible Bayesian nonparametric modelling approach that has been widely applied to learning tasks such as facial expression recognition, image reconstruction, and human pose estimation. To address the issues of poor scaling from exact inference methods, approximation methods based on sparse Gaussian processes (SGP) and variational inference (VI) are necessary for the inference on large datasets. However, one of the problems involved in SGP, especially in latent variable models, is that the distribution of the inducing inputs may fail to capture the distribution of training inputs, which may lead to inefficient inference and poor model prediction. Hence, we propose a regularization approach for sparse Gaussian processes. We also extend this regularization approach into latent sparse Gaussian processes in a unified view, considering the balance of the distribution of inducing inputs and embedding inputs. Furthermore, we justify that performing VI on a sparse latent Gaussian process with this regularization term is equivalent to performing VI on a related empirical Bayes model with a prior on the inducing inputs. Also stochastic variational inference is available for our regularization approach. Finally, the feasibility of our proposed regularization method is demonstrated on three real-world datasets.