Regularized Sparse Gaussian Processes

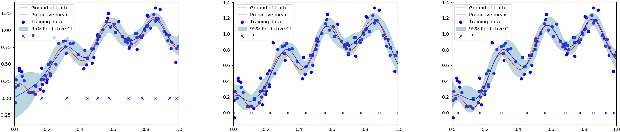
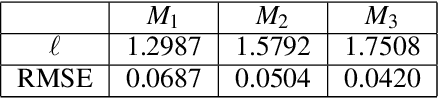
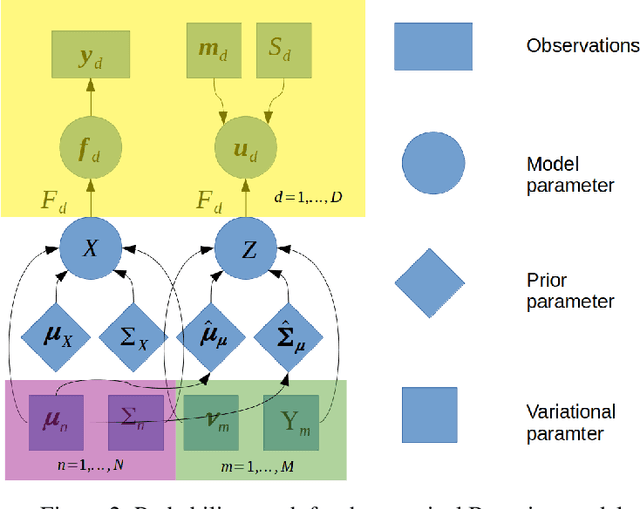
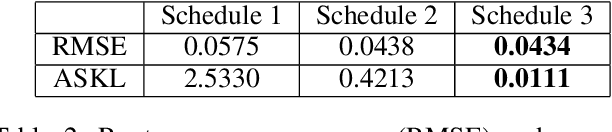
Gaussian processes are a flexible Bayesian nonparametric modelling approach that has been widely applied to learning tasks such as facial expression recognition, image reconstruction, and human pose estimation. To address the issues of poor scaling from exact inference methods, approximation methods based on sparse Gaussian processes (SGP) and variational inference (VI) are necessary for the inference on large datasets. However, one of the problems involved in SGP, especially in latent variable models, is that the distribution of the inducing inputs may fail to capture the distribution of training inputs, which may lead to inefficient inference and poor model prediction. Hence, we propose a regularization approach for sparse Gaussian processes. We also extend this regularization approach into latent sparse Gaussian processes in a unified view, considering the balance of the distribution of inducing inputs and embedding inputs. Furthermore, we justify that performing VI on a sparse latent Gaussian process with this regularization term is equivalent to performing VI on a related empirical Bayes model with a prior on the inducing inputs. Also stochastic variational inference is available for our regularization approach. Finally, the feasibility of our proposed regularization method is demonstrated on three real-world datasets.