Hierarchical Hidden Markov Jump Processes for Cancer Screening Modeling
Paper and Code
Oct 13, 2019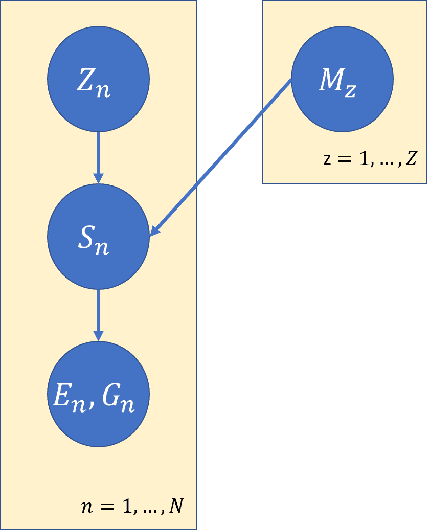
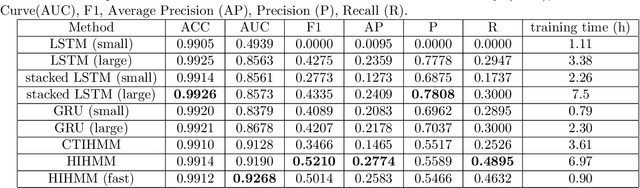
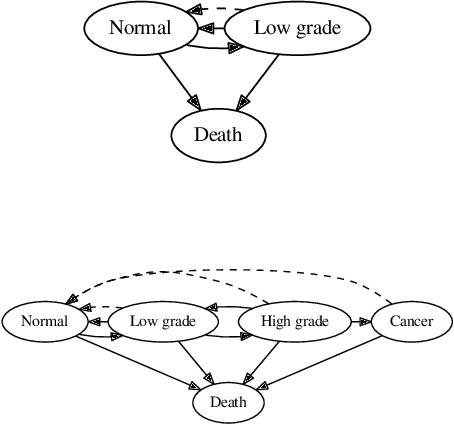
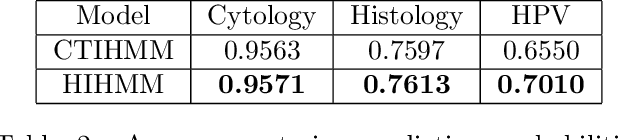
Hidden Markov jump processes are an attractive approach for modeling clinical disease progression data because they are explainable and capable of handling both irregularly sampled and noisy data. Most applications in this context consider time-homogeneous models due to their relative computational simplicity. However, the time homogeneous assumption is too strong to accurately model the natural history of many diseases. Moreover, the population at risk is not homogeneous either, since disease exposure and susceptibility can vary considerably. In this paper, we propose a piece-wise stationary transition matrix to explain the heterogeneity in time. We propose a hierarchical structure for the heterogeneity in population, where prior information is considered to deal with unbalanced data. Moreover, an efficient, scalable EM algorithm is proposed for inference. We demonstrate the feasibility and superiority of our model on a cervical cancer screening dataset from the Cancer Registry of Norway. Experiments show that our model outperforms state-of-the-art recurrent neural network models in terms of prediction accuracy and significantly outperforms a standard hidden Markov jump process in generating Kaplan-Meier estimators.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge