The Geometry of Alignment Collapse: When Fine-Tuning Breaks Safety

Fine-tuning aligned language models on benign tasks unpredictably degrades safety guardrails, even when training data contains no harmful content and developers have no adversarial intent. We show that the prevailing explanation, that fine-tuning updates should be orthogonal to safety-critical directions in high-dimensional parameter space, offers false reassurance: we show this orthogonality is structurally unstable and collapses under the dynamics of gradient descent. We then resolve this through a novel geometric analysis, proving that alignment concentrates in low-dimensional subspaces with sharp curvature, creating a brittle structure that first-order methods cannot detect or defend. While initial fine-tuning updates may indeed avoid these subspaces, the curvature of the fine-tuning loss generates second-order acceleration that systematically steers trajectories into alignment-sensitive regions. We formalize this mechanism through the Alignment Instability Condition, three geometric properties that, when jointly satisfied, lead to safety degradation. Our main result establishes a quartic scaling law: alignment loss grows with the fourth power of training time, governed by the sharpness of alignment geometry and the strength of curvature coupling between the fine-tuning task and safety-critical parameters. These results expose a structural blind spot in the current safety paradigm. The dominant approaches to safe fine-tuning address only the initial snapshot of a fundamentally dynamic problem. Alignment fragility is not a bug to be patched; it is an intrinsic geometric property of gradient descent on curved manifolds. Our results motivate the development of curvature-aware methods, and we hope will further enable a shift in alignment safety analysis from reactive red-teaming to predictive diagnostics for open-weight model deployment.

Matched Pair Calibration for Ranking Fairness

We propose a test of fairness in score-based ranking systems called matched pair calibration. Our approach constructs a set of matched item pairs with minimal confounding differences between subgroups before computing an appropriate measure of ranking error over the set. The matching step ensures that we compare subgroup outcomes between identically scored items so that measured performance differences directly imply unfairness in subgroup-level exposures. We show how our approach generalizes the fairness intuitions of calibration from a binary classification setting to ranking and connect our approach to other proposals for ranking fairness measures. Moreover, our strategy shows how the logic of marginal outcome tests extends to cases where the analyst has access to model scores. Lastly, we provide an example of applying matched pair calibration to a real-word ranking data set to demonstrate its efficacy in detecting ranking bias.

Enforcing Delayed-Impact Fairness Guarantees

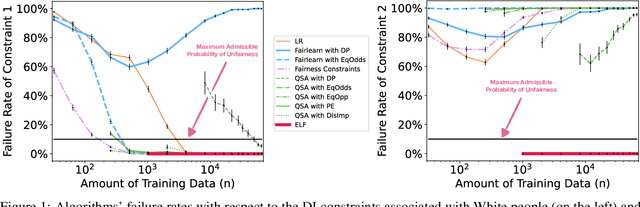
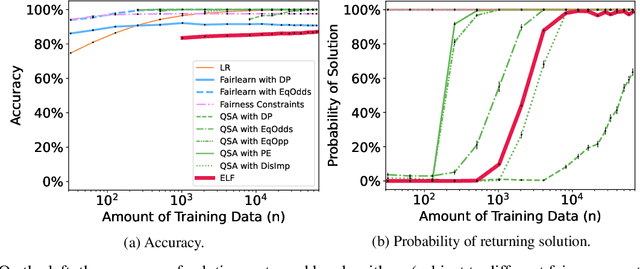
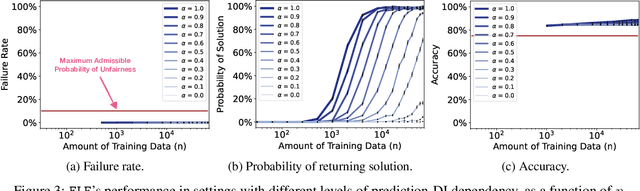
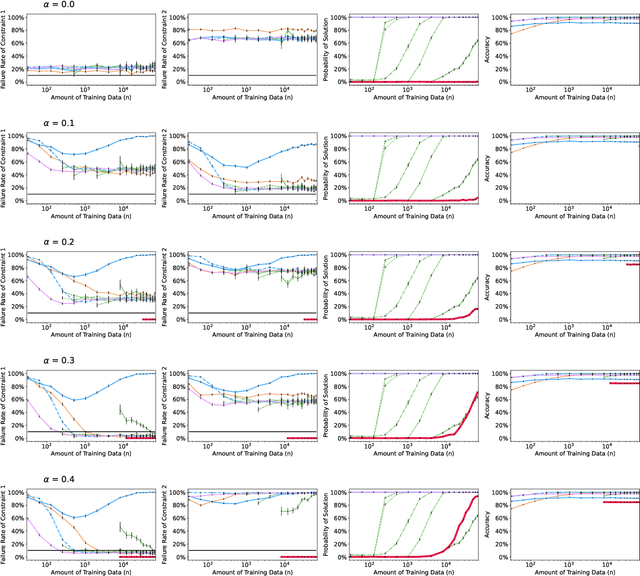
Recent research has shown that seemingly fair machine learning models, when used to inform decisions that have an impact on peoples' lives or well-being (e.g., applications involving education, employment, and lending), can inadvertently increase social inequality in the long term. This is because prior fairness-aware algorithms only consider static fairness constraints, such as equal opportunity or demographic parity. However, enforcing constraints of this type may result in models that have negative long-term impact on disadvantaged individuals and communities. We introduce ELF (Enforcing Long-term Fairness), the first classification algorithm that provides high-confidence fairness guarantees in terms of long-term, or delayed, impact. We prove that the probability that ELF returns an unfair solution is less than a user-specified tolerance and that (under mild assumptions), given sufficient training data, ELF is able to find and return a fair solution if one exists. We show experimentally that our algorithm can successfully mitigate long-term unfairness.

Reinforcement Learning When All Actions are Not Always Available

The Markov decision process (MDP) formulation used to model many real-world sequential decision making problems does not capture the setting where the set of available decisions (actions) at each time step is stochastic. Recently, the stochastic action set Markov decision process (SAS-MDP) formulation has been proposed, which captures the concept of a stochastic action set. In this paper we argue that existing RL algorithms for SAS-MDPs suffer from divergence issues, and present new algorithms for SAS-MDPs that incorporate variance reduction techniques unique to this setting, and provide conditions for their convergence. We conclude with experiments that demonstrate the practicality of our approaches using several tasks inspired by real-life use cases wherein the action set is stochastic.