Biqing Fang
Structural Similarity of Boundary Conditions and an Efficient Local Search Algorithm for Goal Conflict Identification
Feb 23, 2021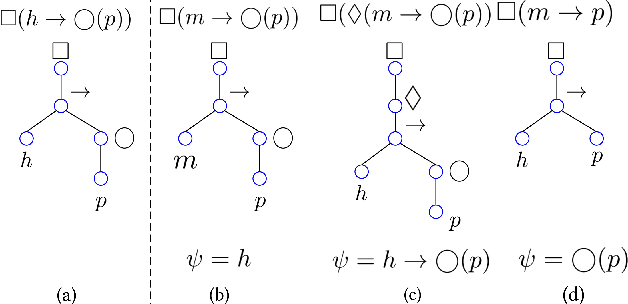
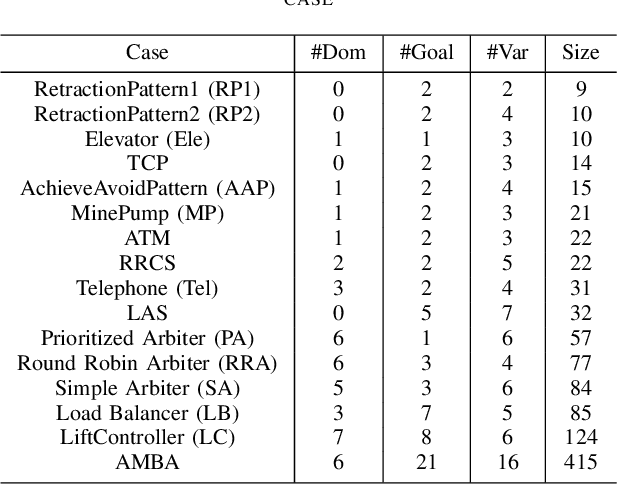
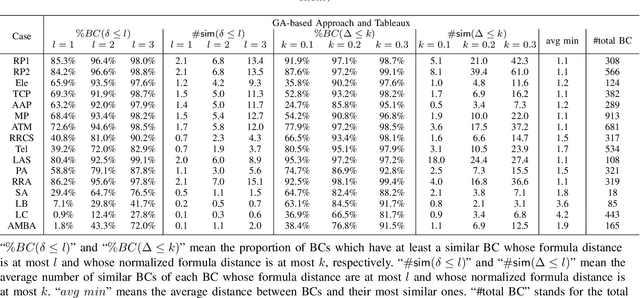
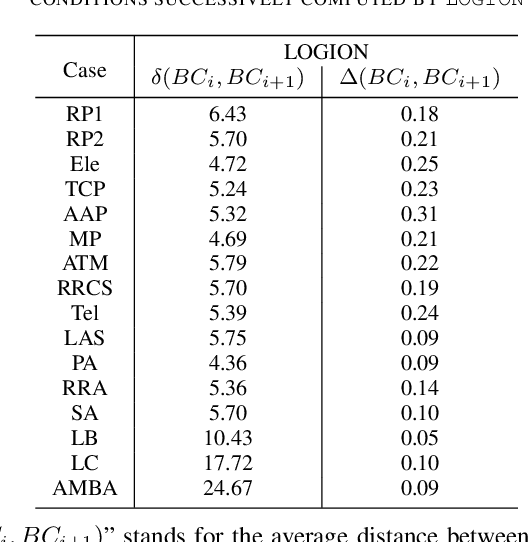
Abstract:In goal-oriented requirements engineering, goal conflict identification is of fundamental importance for requirements analysis. The task aims to find the feasible situations which make the goals diverge within the domain, called boundary conditions (BCs). However, the existing approaches for goal conflict identification fail to find sufficient BCs and general BCs which cover more combinations of circumstances. From the BCs found by these existing approaches, we have observed an interesting phenomenon that there are some pairs of BCs are similar in formula structure, which occurs frequently in the experimental cases. In other words, once a BC is found, a new BC may be discovered quickly by slightly changing the former. It inspires us to develop a local search algorithm named LOGION to find BCs, in which the structural similarity is captured by the neighborhood relation of formulae. Based on structural similarity, LOGION can find a lot of BCs in a short time. Moreover, due to the large number of BCs identified, it potentially selects more general BCs from them. By taking experiments on a set of cases, we show that LOGION effectively exploits the structural similarity of BCs. We also compare our algorithm against the two state-of-the-art approaches. The experimental results show that LOGION produces one order of magnitude more BCs than the state-of-the-art approaches and confirm that LOGION finds out more general BCs thanks to a large number of BCs.
A General Multi-agent Epistemic Planner Based on Higher-order Belief Change
Aug 14, 2018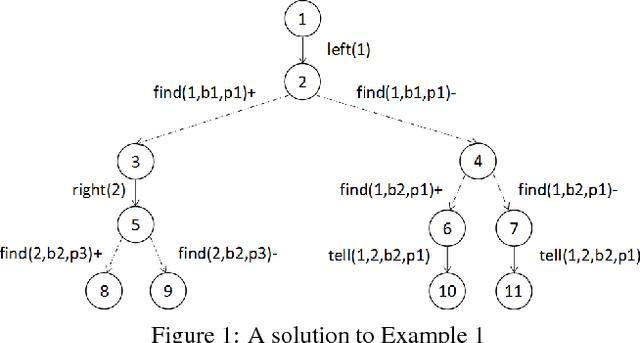
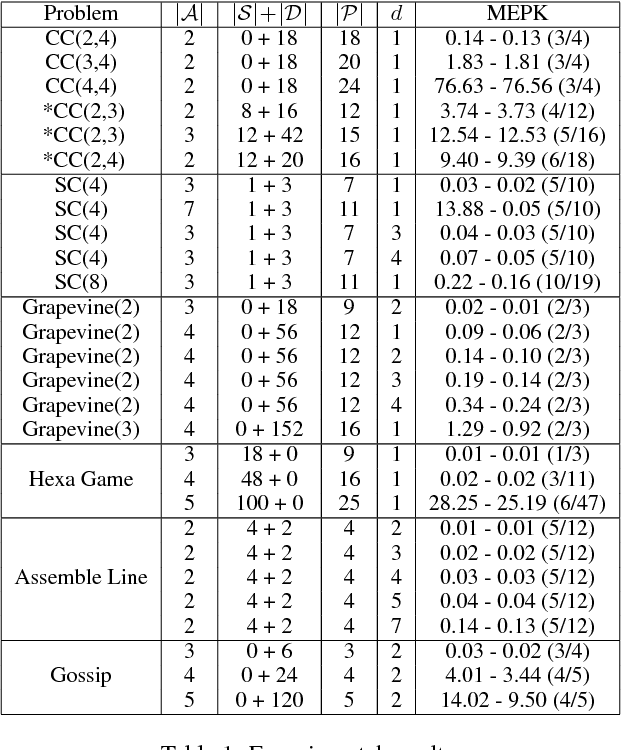
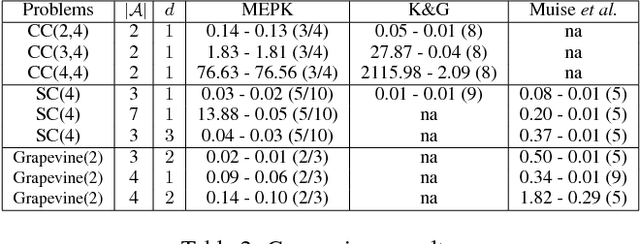
Abstract:In recent years, multi-agent epistemic planning has received attention from both dynamic logic and planning communities. Existing implementations of multi-agent epistemic planning are based on compilation into classical planning and suffer from various limitations, such as generating only linear plans, restriction to public actions, and incapability to handle disjunctive beliefs. In this paper, we propose a general representation language for multi-agent epistemic planning where the initial KB and the goal, the preconditions and effects of actions can be arbitrary multi-agent epistemic formulas, and the solution is an action tree branching on sensing results. To support efficient reasoning in the multi-agent KD45 logic, we make use of a normal form called alternating cover disjunctive formulas (ACDFs). We propose basic revision and update algorithms for ACDFs. We also handle static propositional common knowledge, which we call constraints. Based on our reasoning, revision and update algorithms, adapting the PrAO algorithm for contingent planning from the literature, we implemented a multi-agent epistemic planner called MEPK. Our experimental results show the viability of our approach.
* One of the authors think it's not appropriate to show this work there days. Then we discussed, we want submit a new work and this one together later
Dependence in Propositional Logic: Formula-Formula Dependence and Formula Forgetting -- Application to Belief Update and Conservative Extension
Jun 29, 2018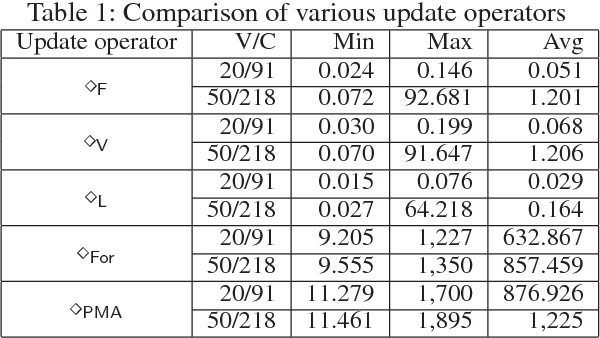
Abstract:Dependence is an important concept for many tasks in artificial intelligence. A task can be executed more efficiently by discarding something independent from the task. In this paper, we propose two novel notions of dependence in propositional logic: formula-formula dependence and formula forgetting. The first is a relation between formulas capturing whether a formula depends on another one, while the second is an operation that returns the strongest consequence independent of a formula. We also apply these two notions in two well-known issues: belief update and conservative extension. Firstly, we define a new update operator based on formula-formula dependence. Furthermore, we reduce conservative extension to formula forgetting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge