Structural Similarity of Boundary Conditions and an Efficient Local Search Algorithm for Goal Conflict Identification

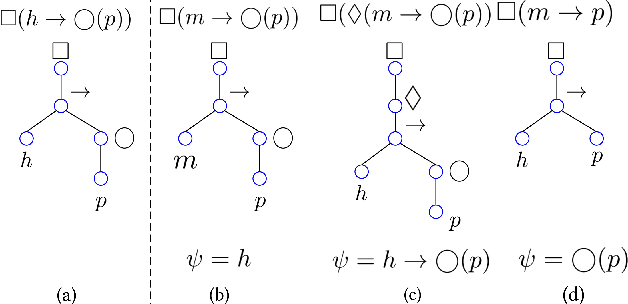
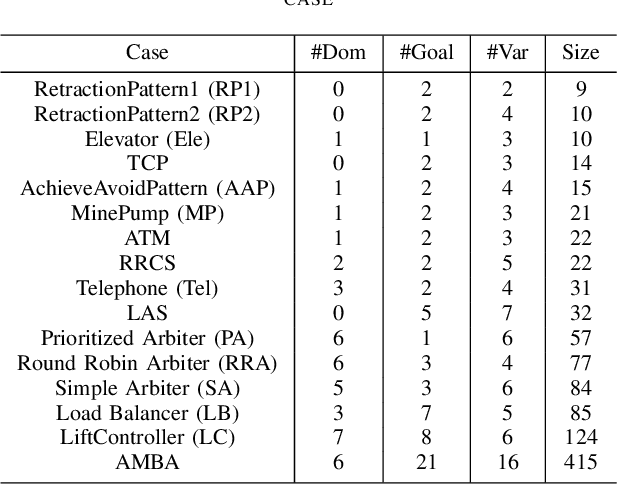
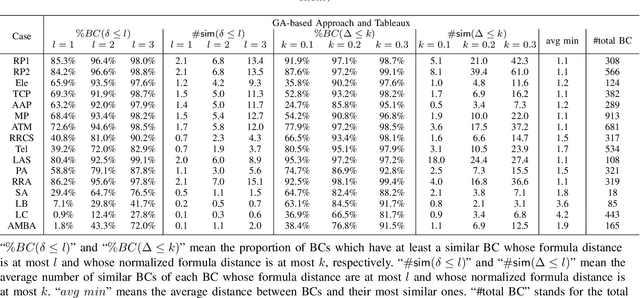
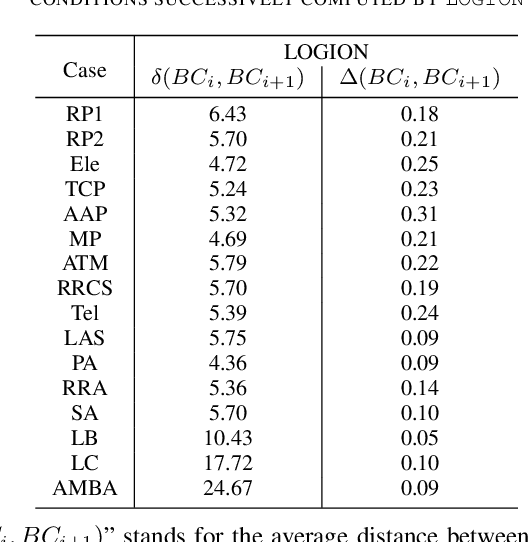
In goal-oriented requirements engineering, goal conflict identification is of fundamental importance for requirements analysis. The task aims to find the feasible situations which make the goals diverge within the domain, called boundary conditions (BCs). However, the existing approaches for goal conflict identification fail to find sufficient BCs and general BCs which cover more combinations of circumstances. From the BCs found by these existing approaches, we have observed an interesting phenomenon that there are some pairs of BCs are similar in formula structure, which occurs frequently in the experimental cases. In other words, once a BC is found, a new BC may be discovered quickly by slightly changing the former. It inspires us to develop a local search algorithm named LOGION to find BCs, in which the structural similarity is captured by the neighborhood relation of formulae. Based on structural similarity, LOGION can find a lot of BCs in a short time. Moreover, due to the large number of BCs identified, it potentially selects more general BCs from them. By taking experiments on a set of cases, we show that LOGION effectively exploits the structural similarity of BCs. We also compare our algorithm against the two state-of-the-art approaches. The experimental results show that LOGION produces one order of magnitude more BCs than the state-of-the-art approaches and confirm that LOGION finds out more general BCs thanks to a large number of BCs.

CoAPI: An Efficient Two-Phase Algorithm Using Core-Guided Over-Approximate Cover for Prime Compilation of Non-Clausal Formulae

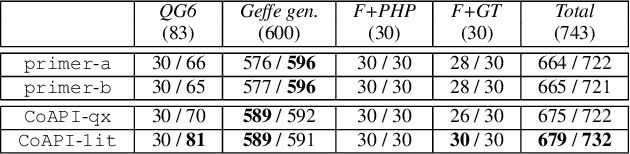
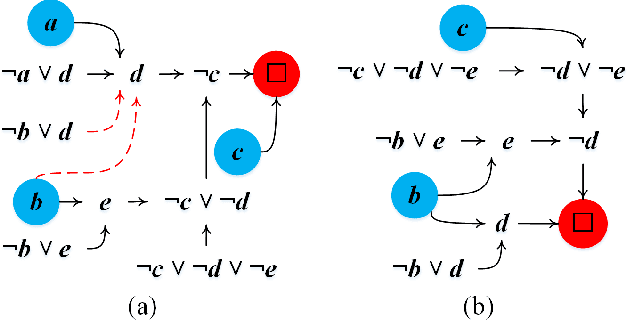
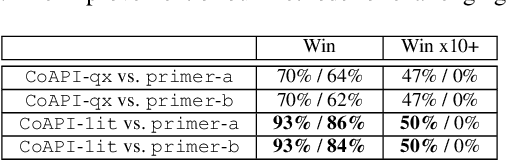
Prime compilation, i.e., the generation of all prime implicates or implicants (primes for short) of formulae, is a prominent fundamental issue for AI. Recently, the prime compilation for non-clausal formulae has received great attention. The state-of-the-art approaches generate all primes along with a prime cover constructed by prime implicates using dual rail encoding. However, the dual rail encoding potentially expands search space. In addition, constructing a prime cover, which is necessary for their methods, is time-consuming. To address these issues, we propose a novel two-phase method -- CoAPI. The two phases are the key to construct a cover without using dual rail encoding. Specifically, given a non-clausal formula, we first propose a core-guided method to rewrite the non-clausal formula into a cover constructed by over-approximate implicates in the first phase. Then, we generate all the primes based on the cover in the second phase. In order to reduce the size of the cover, we provide a multi-order based shrinking method, with a good tradeoff between the small size and efficiency, to compress the size of cover considerably. The experimental results show that CoAPI outperforms state-of-the-art approaches. Particularly, for generating all prime implicates, CoAPI consumes about one order of magnitude less time.