Robust Sequence Networked Submodular Maximization

In this paper, we study the \underline{R}obust \underline{o}ptimization for \underline{se}quence \underline{Net}worked \underline{s}ubmodular maximization (RoseNets) problem. We interweave the robust optimization with the sequence networked submodular maximization. The elements are connected by a directed acyclic graph and the objective function is not submodular on the elements but on the edges in the graph. Under such networked submodular scenario, the impact of removing an element from a sequence depends both on its position in the sequence and in the network. This makes the existing robust algorithms inapplicable. In this paper, we take the first step to study the RoseNets problem. We design a robust greedy algorithm, which is robust against the removal of an arbitrary subset of the selected elements. The approximation ratio of the algorithm depends both on the number of the removed elements and the network topology. We further conduct experiments on real applications of recommendation and link prediction. The experimental results demonstrate the effectiveness of the proposed algorithm.

Unrestricted Adversarial Attacks on ImageNet Competition

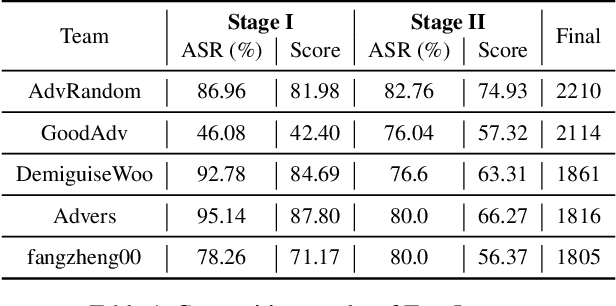
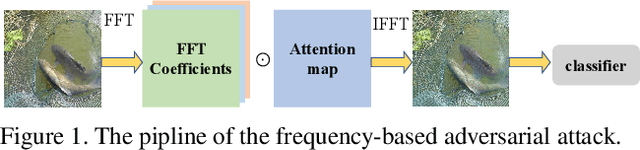
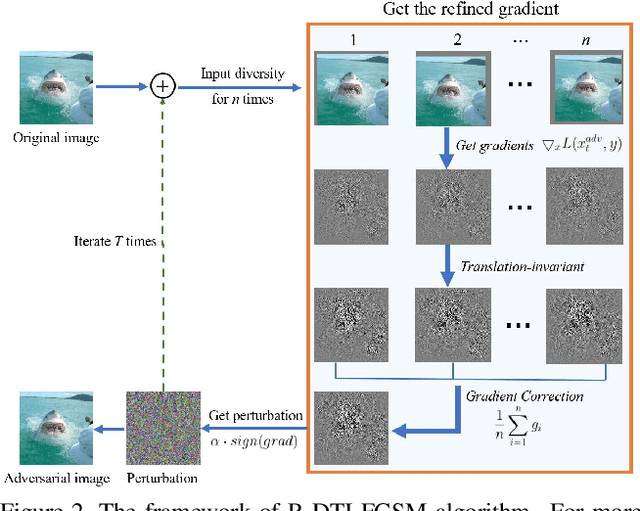
Many works have investigated the adversarial attacks or defenses under the settings where a bounded and imperceptible perturbation can be added to the input. However in the real-world, the attacker does not need to comply with this restriction. In fact, more threats to the deep model come from unrestricted adversarial examples, that is, the attacker makes large and visible modifications on the image, which causes the model classifying mistakenly, but does not affect the normal observation in human perspective. Unrestricted adversarial attack is a popular and practical direction but has not been studied thoroughly. We organize this competition with the purpose of exploring more effective unrestricted adversarial attack algorithm, so as to accelerate the academical research on the model robustness under stronger unbounded attacks. The competition is held on the TianChi platform (\url{https://tianchi.aliyun.com/competition/entrance/531853/introduction}) as one of the series of AI Security Challengers Program.