Rethinking Class Activation Maps for Segmentation: Revealing Semantic Information in Shallow Layers by Reducing Noise

Class activation maps are widely used for explaining deep neural networks. Due to its ability to highlight regions of interest, it has evolved in recent years as a key step in weakly supervised learning. A major limitation to the performance of the class activation maps is the small spatial resolution of the feature maps in the last layer of the convolutional neural network. Therefore, we expect to generate high-resolution feature maps that result in high-quality semantic information. In this paper, we rethink the properties of semantic information in shallow feature maps. We find that the shallow feature maps still have fine-grained non-discriminative features while mixing considerable non-target noise. Furthermore, we propose a simple gradient-based denoising method to filter the noise by truncating the positive gradient. Our proposed scheme can be easily deployed in other CAM-related methods, facilitating these methods to obtain higher-quality class activation maps. We evaluate the proposed approach through a weakly-supervised semantic segmentation task, and a large number of experiments demonstrate the effectiveness of our approach.

SAL-CNN: Estimate the Remaining Useful Life of Bearings Using Time-frequency Information

In modern industrial production, the prediction ability of the remaining useful life (RUL) of bearings directly affects the safety and stability of the system. Traditional methods require rigorous physical modeling and perform poorly for complex systems. In this paper, an end-to-end RUL prediction method is proposed, which uses short-time Fourier transform (STFT) as preprocessing. Considering the time correlation of signal sequences, a long and short-term memory network is designed in CNN, incorporating the convolutional block attention module, and understanding the decision-making process of the network from the interpretability level. Experiments were carried out on the 2012PHM dataset and compared with other methods, and the results proved the effectiveness of the method.

Training Neural Networks for Solving 1-D Optimal Piecewise Linear Approximation

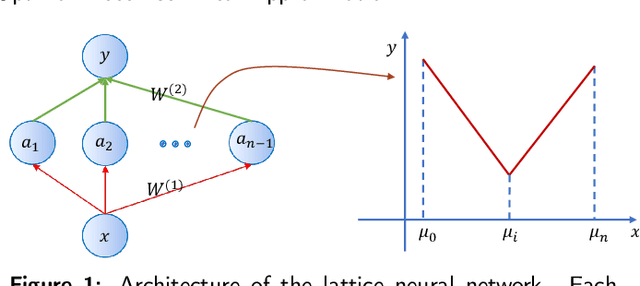
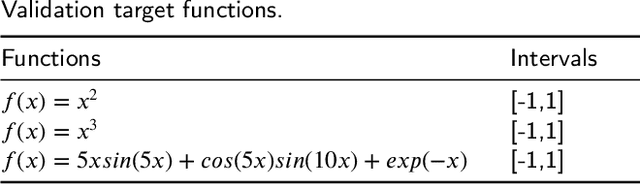
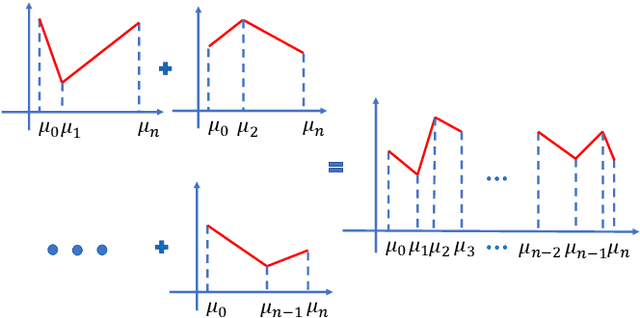
Recently, the interpretability of deep learning has attracted a lot of attention. A plethora of methods have attempted to explain neural networks by feature visualization, saliency maps, model distillation, and so on. However, it is hard for these methods to reveal the intrinsic properties of neural networks. In this work, we studied the 1-D optimal piecewise linear approximation (PWLA) problem, and associated it with a designed neural network, named lattice neural network (LNN). We asked four essential questions as following: (1) What are the characters of the optimal solution of the PWLA problem? (2) Can an LNN converge to the global optimum? (3) Can an LNN converge to the local optimum? (4) Can an LNN solve the PWLA problem? Our main contributions are that we propose the theorems to characterize the optimal solution of the PWLA problem and present the LNN method for solving it. We evaluated the proposed LNNs on approximation tasks, forged an empirical method to improve the performance of LNNs. The experiments verified that our LNN method is competitive with the start-of-the-art method.

How to Explain Neural Networks: A perspective of data space division

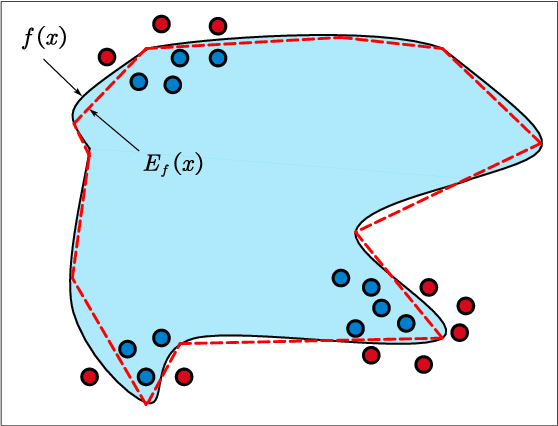
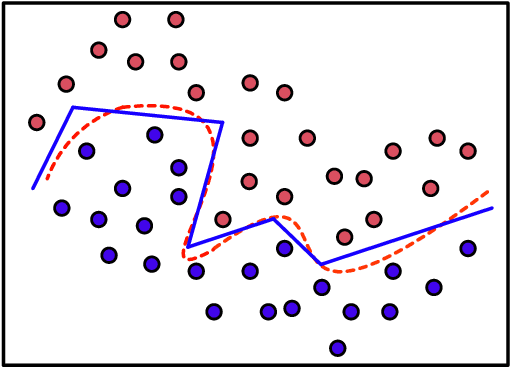
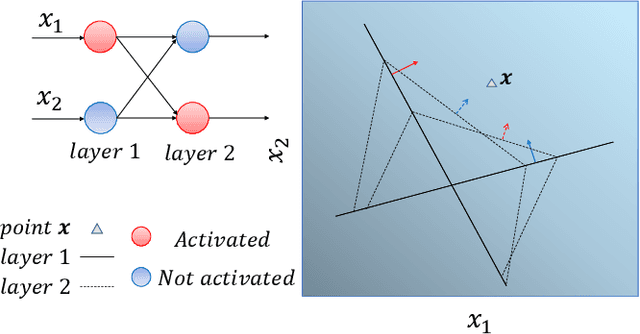
Interpretability of intelligent algorithms represented by deep learning has been yet an open problem. We discuss the shortcomings of the existing explainable method based on the two attributes of explanation, which are called completeness and explicitness. Furthermore, we point out that a model that completely relies on feed-forward mapping is extremely easy to cause inexplicability because it is hard to quantify the relationship between this mapping and the final model. Based on the perspective of the data space division, the principle of complete local interpretable model-agnostic explanations (CLIMEP) is proposed in this paper. To study the classification problems, we further discussed the equivalence of the CLIMEP and the decision boundary. As a matter of fact, it is also difficult to implementation of CLIMEP. To tackle the challenge, motivated by the fact that a fully-connected neural network (FCNN) with piece-wise linear activation functions (PWLs) can partition the input space into several linear regions, we extend this result to arbitrary FCNNs by the strategy of linearizing the activation functions. Applying this technique to solving classification problems, it is the first time that the complete decision boundary of FCNNs has been able to be obtained. Finally, we propose the DecisionNet (DNet), which divides the input space by the hyper-planes of the decision boundary. Hence, each linear interval of the DNet merely contains samples of the same label. Experiments show that the surprising model compression efficiency of the DNet with an arbitrary controlled precision.