Training Neural Networks for Solving 1-D Optimal Piecewise Linear Approximation
Paper and Code
Oct 14, 2021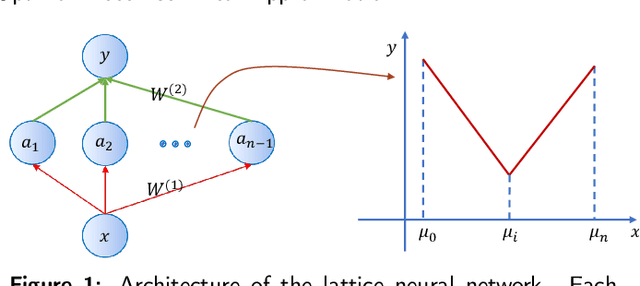
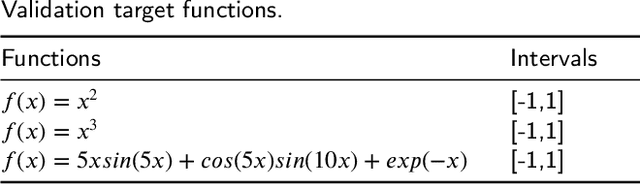
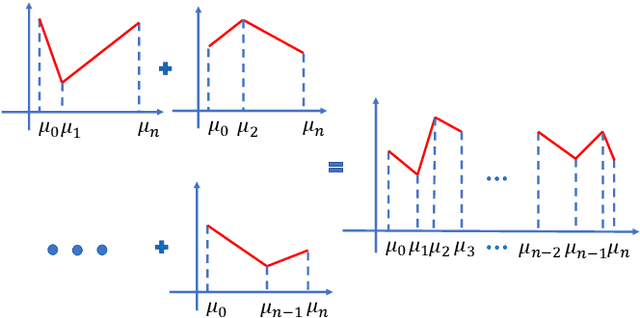

Recently, the interpretability of deep learning has attracted a lot of attention. A plethora of methods have attempted to explain neural networks by feature visualization, saliency maps, model distillation, and so on. However, it is hard for these methods to reveal the intrinsic properties of neural networks. In this work, we studied the 1-D optimal piecewise linear approximation (PWLA) problem, and associated it with a designed neural network, named lattice neural network (LNN). We asked four essential questions as following: (1) What are the characters of the optimal solution of the PWLA problem? (2) Can an LNN converge to the global optimum? (3) Can an LNN converge to the local optimum? (4) Can an LNN solve the PWLA problem? Our main contributions are that we propose the theorems to characterize the optimal solution of the PWLA problem and present the LNN method for solving it. We evaluated the proposed LNNs on approximation tasks, forged an empirical method to improve the performance of LNNs. The experiments verified that our LNN method is competitive with the start-of-the-art method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge