Retinal Microaneurysms Detection using Local Convergence Index Features

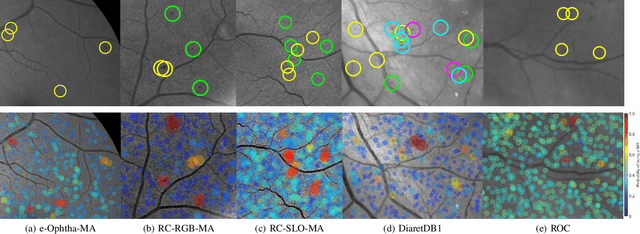
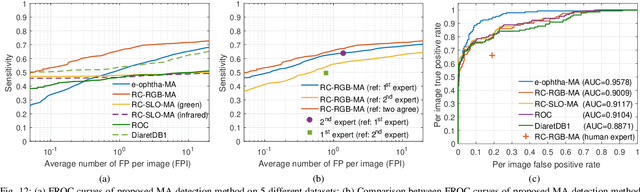
Retinal microaneurysms are the earliest clinical sign of diabetic retinopathy disease. Detection of microaneurysms is crucial for the early diagnosis of diabetic retinopathy and prevention of blindness. In this paper, a novel and reliable method for automatic detection of microaneurysms in retinal images is proposed. In the first stage of the proposed method, several preliminary microaneurysm candidates are extracted using a gradient weighting technique and an iterative thresholding approach. In the next stage, in addition to intensity and shape descriptors, a new set of features based on local convergence index filters is extracted for each candidate. Finally, the collective set of features is fed to a hybrid sampling/boosting classifier to discriminate the MAs from non-MAs candidates. The method is evaluated on images with different resolutions and modalities (RGB and SLO) using five publicly available datasets including the Retinopathy Online Challenge's dataset. The proposed method achieves an average sensitivity score of 0.471 on the ROC dataset outperforming state-of-the-art approaches in an extensive comparison. The experimental results on the other four datasets demonstrate the effectiveness and robustness of the proposed microaneurysms detection method regardless of different image resolutions and modalities.

Curvature Integration in a 5D Kernel for Extracting Vessel Connections in Retinal Images

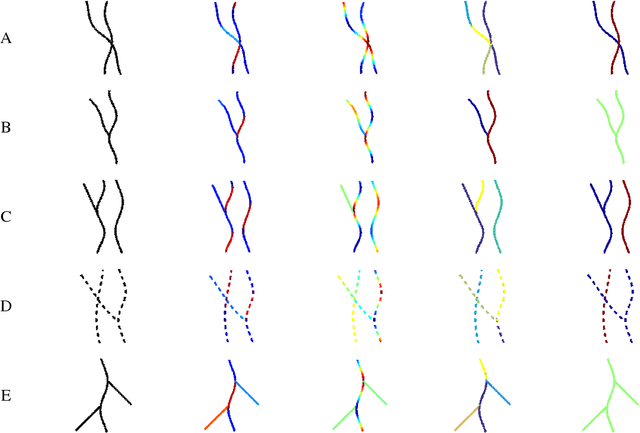
Tree-like structures such as retinal images are widely studied in computer-aided diagnosis systems for large-scale screening programs. Despite several segmentation and tracking methods proposed in the literature, there still exist several limitations specifically when two or more curvilinear structures cross or bifurcate, or in the presence of interrupted lines or highly curved blood vessels. In this paper, we propose a novel approach based on multi-orientation scores augmented with a contextual affinity matrix, which both are inspired by the geometry of the primary visual cortex (V1) and their contextual connections. The connectivity is described with a five-dimensional kernel obtained as the fundamental solution of the Fokker-Planck equation modelling the cortical connectivity in the lifted space of positions, orientations, curvatures and intensity. It is further used in a self-tuning spectral clustering step to identify the main perceptual units in the stimuli. The proposed method has been validated on several easy and challenging structures in a set of artificial images and actual retinal patches. Supported by quantitative and qualitative results, the method is capable of overcoming the limitations of current state-of-the-art techniques.

Template Matching via Densities on the Roto-Translation Group

We propose a template matching method for the detection of 2D image objects that are characterized by orientation patterns. Our method is based on data representations via orientation scores, which are functions on the space of positions and orientations, and which are obtained via a wavelet-type transform. This new representation allows us to detect orientation patterns in an intuitive and direct way, namely via cross-correlations. Additionally, we propose a generalized linear regression framework for the construction of suitable templates using smoothing splines. Here, it is important to recognize a curved geometry on the position-orientation domain, which we identify with the Lie group SE(2): the roto-translation group. Templates are then optimized in a B-spline basis, and smoothness is defined with respect to the curved geometry. We achieve state-of-the-art results on three different applications: detection of the optic nerve head in the retina (99.83% success rate on 1737 images), of the fovea in the retina (99.32% success rate on 1616 images), and of the pupil in regular camera images (95.86% on 1521 images). The high performance is due to inclusion of both intensity and orientation features with effective geometric priors in the template matching. Moreover, our method is fast due to a cross-correlation based matching approach.

Numerical Approaches for Linear Left-invariant Diffusions on SE(2), their Comparison to Exact Solutions, and their Applications in Retinal Imaging

Left-invariant PDE-evolutions on the roto-translation group $SE(2)$ (and their resolvent equations) have been widely studied in the fields of cortical modeling and image analysis. They include hypo-elliptic diffusion (for contour enhancement) proposed by Citti & Sarti, and Petitot, and they include the direction process (for contour completion) proposed by Mumford. This paper presents a thorough study and comparison of the many numerical approaches, which, remarkably, is missing in the literature. Existing numerical approaches can be classified into 3 categories: Finite difference methods, Fourier based methods (equivalent to $SE(2)$-Fourier methods), and stochastic methods (Monte Carlo simulations). There are also 3 types of exact solutions to the PDE-evolutions that were derived explicitly (in the spatial Fourier domain) in previous works by Duits and van Almsick in 2005. Here we provide an overview of these 3 types of exact solutions and explain how they relate to each of the 3 numerical approaches. We compute relative errors of all numerical approaches to the exact solutions, and the Fourier based methods show us the best performance with smallest relative errors. We also provide an improvement of Mathematica algorithms for evaluating Mathieu-functions, crucial in implementations of the exact solutions. Furthermore, we include an asymptotical analysis of the singularities within the kernels and we propose a probabilistic extension of underlying stochastic processes that overcomes the singular behavior in the origin of time-integrated kernels. Finally, we show retinal imaging applications of combining left-invariant PDE-evolutions with invertible orientation scores.

A Two-Stage Combined Classifier in Scale Space Texture Classification

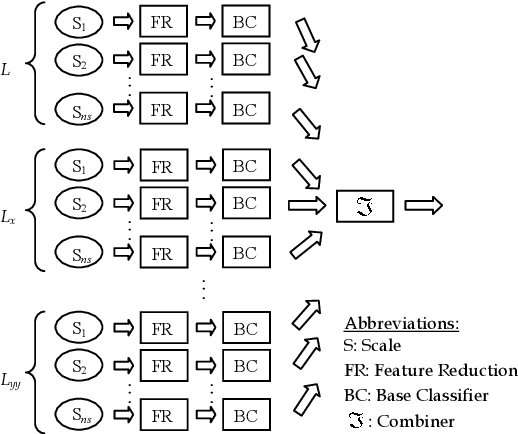
Textures often show multiscale properties and hence multiscale techniques are considered useful for texture analysis. Scale-space theory as a biologically motivated approach may be used to construct multiscale textures. In this paper various ways are studied to combine features on different scales for texture classification of small image patches. We use the N-jet of derivatives up to the second order at different scales to generate distinct pattern representations (DPR) of feature subsets. Each feature subset in the DPR is given to a base classifier (BC) of a two-stage combined classifier. The decisions made by these BCs are combined in two stages over scales and derivatives. Various combining systems and their significances and differences are discussed. The learning curves are used to evaluate the performances. We found for small sample sizes combining classifiers performs significantly better than combining feature spaces (CFS). It is also shown that combining classifiers performs better than the support vector machine on CFS in multiscale texture classification.