Curvature Integration in a 5D Kernel for Extracting Vessel Connections in Retinal Images

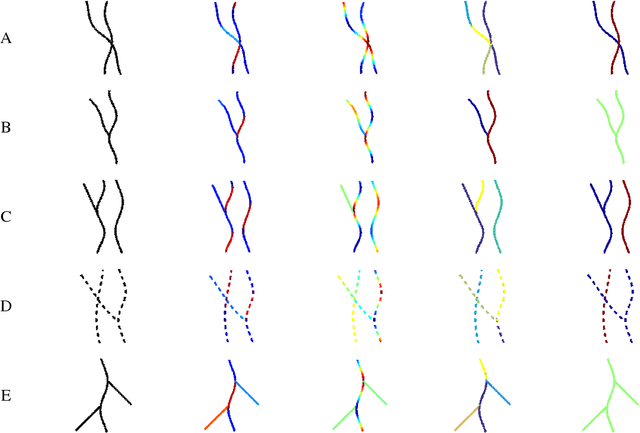
Tree-like structures such as retinal images are widely studied in computer-aided diagnosis systems for large-scale screening programs. Despite several segmentation and tracking methods proposed in the literature, there still exist several limitations specifically when two or more curvilinear structures cross or bifurcate, or in the presence of interrupted lines or highly curved blood vessels. In this paper, we propose a novel approach based on multi-orientation scores augmented with a contextual affinity matrix, which both are inspired by the geometry of the primary visual cortex (V1) and their contextual connections. The connectivity is described with a five-dimensional kernel obtained as the fundamental solution of the Fokker-Planck equation modelling the cortical connectivity in the lifted space of positions, orientations, curvatures and intensity. It is further used in a self-tuning spectral clustering step to identify the main perceptual units in the stimuli. The proposed method has been validated on several easy and challenging structures in a set of artificial images and actual retinal patches. Supported by quantitative and qualitative results, the method is capable of overcoming the limitations of current state-of-the-art techniques.

Local and global gestalt laws: A neurally based spectral approach

A mathematical model of figure-ground articulation is presented, taking into account both local and global gestalt laws. The model is compatible with the functional architecture of the primary visual cortex (V1). Particularly the local gestalt law of good continuity is described by means of suitable connectivity kernels, that are derived from Lie group theory and are neurally implemented in long range connectivity in V1. Different kernels are compatible with the geometric structure of cortical connectivity and they are derived as the fundamental solutions of the Fokker Planck, the Sub-Riemannian Laplacian and the isotropic Laplacian equations. The kernels are used to construct matrices of connectivity among the features present in a visual stimulus. Global gestalt constraints are then introduced in terms of spectral analysis of the connectivity matrix, showing that this processing can be cortically implemented in V1 by mean field neural equations. This analysis performs grouping of local features and individuates perceptual units with the highest saliency. Numerical simulations are performed and results are obtained applying the technique to a number of stimuli.

Analysis of Vessel Connectivities in Retinal Images by Cortically Inspired Spectral Clustering

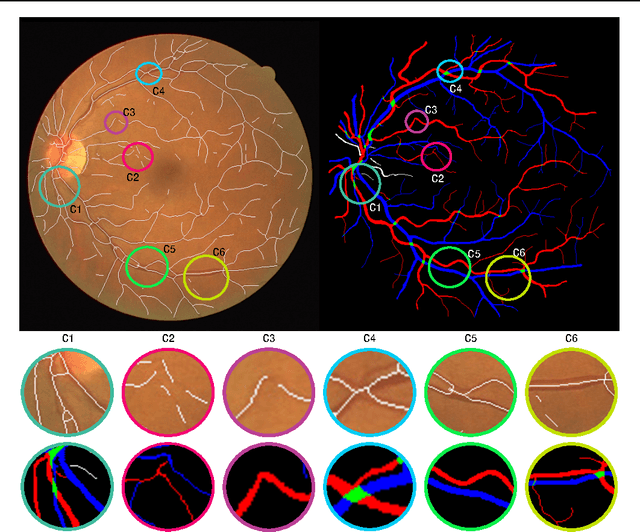
Retinal images provide early signs of diabetic retinopathy, glaucoma, and hypertension. These signs can be investigated based on microaneurysms or smaller vessels. The diagnostic biomarkers are the change of vessel widths and angles especially at junctions, which are investigated using the vessel segmentation or tracking. Vessel paths may also be interrupted; crossings and bifurcations may be disconnected. This paper addresses a novel contextual method based on the geometry of the primary visual cortex (V1) to study these difficulties. We have analyzed the specific problems at junctions with a connectivity kernel obtained as the fundamental solution of the Fokker-Planck equation, which is usually used to represent the geometrical structure of multi-orientation cortical connectivity. Using the spectral clustering on a large local affinity matrix constructed by both the connectivity kernel and the feature of intensity, the vessels are identified successfully in a hierarchical topology each representing an individual perceptual unit.