Retrieving challenging vessel connections in retinal images by line co-occurrence statistics

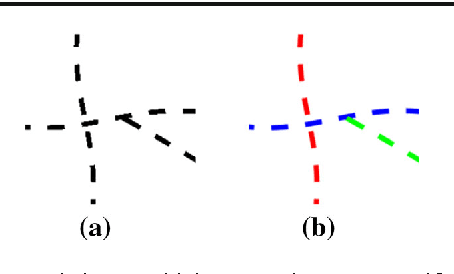
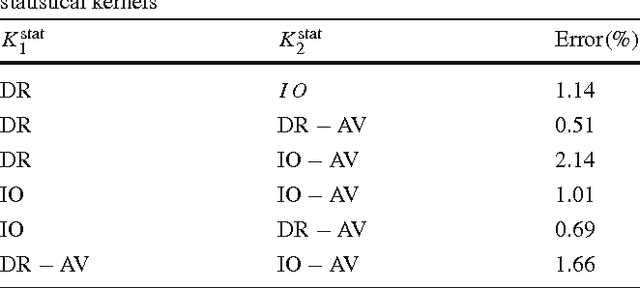
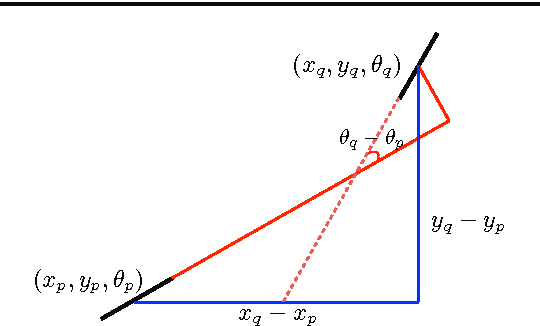
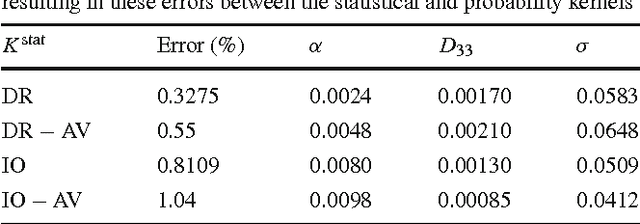
Natural images contain often curvilinear structures, which might be disconnected, or partly occluded. Recovering the missing connection of disconnected structures is an open issue and needs appropriate geometric reasoning. We propose to find line co-occurrence statistics from the centerlines of blood vessels in retinal images and show its remarkable similarity to a well-known probabilistic model for the connectivity pattern in the primary visual cortex. Furthermore, the probabilistic model is trained from the data via statistics and used for automated grouping of interrupted vessels in a spectral clustering based approach. Several challenging image patches are investigated around junction points, where successful results indicate the perfect match of the trained model to the profiles of blood vessels in retinal images. Also, comparisons among several statistical models obtained from different datasets reveals their high similarity i.e., they are independent of the dataset. On top of that, the best approximation of the statistical model with the symmetrized extension of the probabilistic model on the projective line bundle is found with a least square error smaller than 2%. Apparently, the direction process on the projective line bundle is a good continuation model for vessels in retinal images.

Analysis of Vessel Connectivities in Retinal Images by Cortically Inspired Spectral Clustering

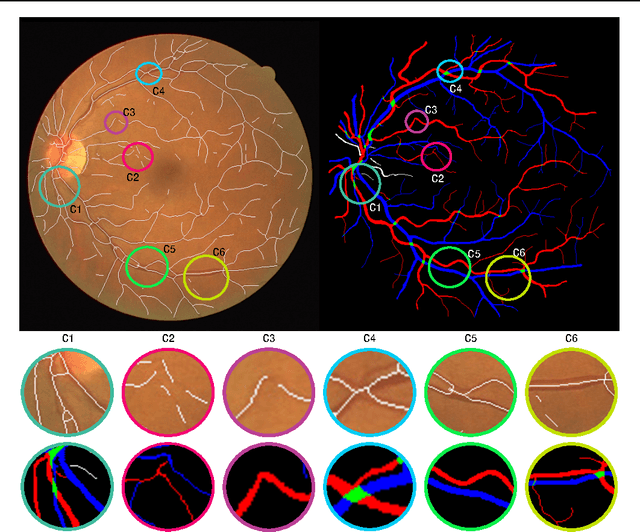
Retinal images provide early signs of diabetic retinopathy, glaucoma, and hypertension. These signs can be investigated based on microaneurysms or smaller vessels. The diagnostic biomarkers are the change of vessel widths and angles especially at junctions, which are investigated using the vessel segmentation or tracking. Vessel paths may also be interrupted; crossings and bifurcations may be disconnected. This paper addresses a novel contextual method based on the geometry of the primary visual cortex (V1) to study these difficulties. We have analyzed the specific problems at junctions with a connectivity kernel obtained as the fundamental solution of the Fokker-Planck equation, which is usually used to represent the geometrical structure of multi-orientation cortical connectivity. Using the spectral clustering on a large local affinity matrix constructed by both the connectivity kernel and the feature of intensity, the vessels are identified successfully in a hierarchical topology each representing an individual perceptual unit.

A Multi-Orientation Analysis Approach to Retinal Vessel Tracking

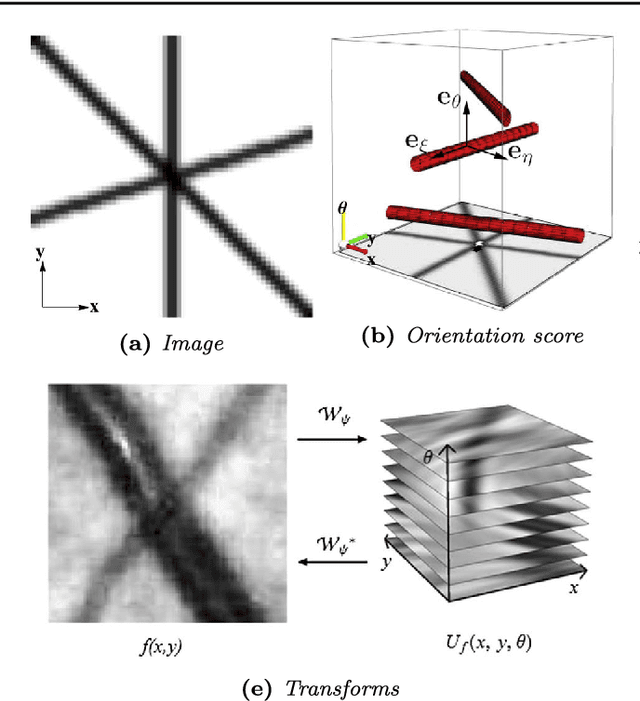
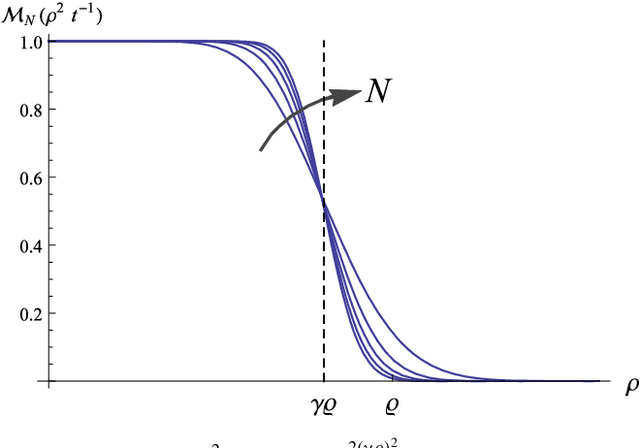
This paper presents a method for retinal vasculature extraction based on biologically inspired multi-orientation analysis. We apply multi-orientation analysis via so-called invertible orientation scores, modeling the cortical columns in the visual system of higher mammals. This allows us to generically deal with many hitherto complex problems inherent to vessel tracking, such as crossings, bifurcations, parallel vessels, vessels of varying widths and vessels with high curvature. Our approach applies tracking in invertible orientation scores via a novel geometrical principle for curve optimization in the Euclidean motion group SE(2). The method runs fully automatically and provides a detailed model of the retinal vasculature, which is crucial as a sound basis for further quantitative analysis of the retina, especially in screening applications.